если правилбно понял задание вот,
ля выполнения своего назначения каждый вид транспорта имеет определенную техническую базу, или иначе, средства производства. Техническое вооружение любого вида транспорта чрезвычайно сложно и многообразно. Главными элементами технического оснащения, характерными для всех видов транспорта, можно считать: путь с искусственными сооружениями (мосты, тоннели, дорожные хозяйства и пр.); подвижной состав; постоянные технические средства, возводимые, как правило, в районах городов и других населенных пунктов в виде станций, портов, вокзалов, депо, грузовых складов (пакгаузов), заводов, мастерских, материально-технических баз, систем энергоснабжения и водоснабжения; специальные (в том числе электронные) устройства для управления движением транспортных единиц и для связи должностных лиц, обслуживающих транспорт. К постоянным техническим средствам относятся также служебные здания и сооружения с соответствующим оборудованием, включая погрузо-разгрузочные машины и механизмы, машины для ремонта и содержания в исправном состоянии всего имущества транспорта.
Исторический опыт показывает, что масштабы транспортного хозяйства в целом растут, причем оснащение непрерывно совершенствуется благодаря новым достижениям науки и техники. Конкретные сведения о названных элементах приводятся ниже при рассмотрении специфики отдельных видов транспорта. Здесь же целесообразно подчеркнуть, что объем и технический уровень оснащения во многом определяют потенциал данного транспорта, но само по себе оно не гарантирует выполнения возложенных на него задач. Для этого необходимы прежде всего адекватная технология, организация и система управления транспортным процессом
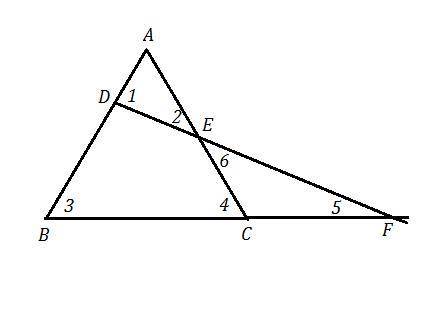
ΔАВС - равнобедренный , АВ=АС ⇒ ∠В=∠АСВ .
Рассм. ΔADE. Чтобы доказать, что АЕ>AD , надо доказать, что ∠ADE>∠AED , так как против бОльшего угла лежит бОльшая сторона .
Рассм. ΔBDF. Внешний угол этого треугольника ∠ADF=∠ADE равен сумме двух углов треугольника, не смежных с ним, то есть
∠ADE=∠B+∠BFD , но ∠В=∠АСВ ⇒ ∠ADE=∠ACB+∠BFD .
Но ∠АСВ - это внешний угол ΔCEF , и поэтому ∠ACB=∠CEF+∠CFE .
Значит, ∠ADE=∠CEF+∠CFE+∠BFD .
Но ∠CFE - это тот же самый угол, что и ∠BFD , ∠CFE=∠BFD .
∠ADE=∠CEF+2*∠CFE
∠CEF=∠AED как вертикальные углы, поэтому
∠ADE=∠AED+2*∠CFE
То есть один ∠ADE равен одному ∠AED плюс ещё два угла ∠CFE , значит ∠ADE>∠AED и сторона, лежащая против ∠ADE (сторона АЕ) больше стороны, лежащей против ∠AED (сторона AD).
AE>AD
Или запись короче, если обозначить углы, как на рисунке:
∠1=∠3+∠5=∠4+∠5=(∠6+∠5)+∠5=∠6+2*∠5=∠2+2*∠5 ⇒
∠1=∠2+2*∠5 , ∠1 >∠2 ⇒ АЕ>AD .
15=10+5
16=10+6
10=10+9