a=400
b=1250
S=ab
S=400*1250
2
S=500000 м
так как 1га=10000м то 500000=50 га
ответ:50 га площадь поля
Обозначим длины сторон данного прямоугольника через х и у.
Согласно условию задачи, площадь данного прямоугольника равна 24 см^12, следовательно, имеет место следующее соотношение:
х * у = 24.
Также известно, что периметр данного прямоугольника равен 20 см, следовательно, имеет место следующее соотношение:
2 * (х + у) = 20.
Решаем полученную систему уравнений.
Из второго уравнения получаем:
х + у = 20 / 10;
х + у = 10;
у = 10 - х.
Подставляя данное значение у = 10 - х в уравнение х * у = 24, получаем:
х * (10 - х) = 24:
10х - х^2 = 24;
х^2 - 10х + 24 = 0;
х = 5 ± √(25 - 24) = 5 ±√1 = 5 ± 1;
х1 = 5 - 1 = 4;
х2 = 5 + 1 = 5.
Находим у:
у1 = 10 - х1 = 10 - 4 = 6;
у2 = 10 - х2 = 10 - 6 = 4.
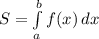
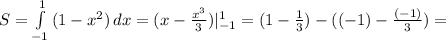
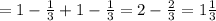 ед².
ед².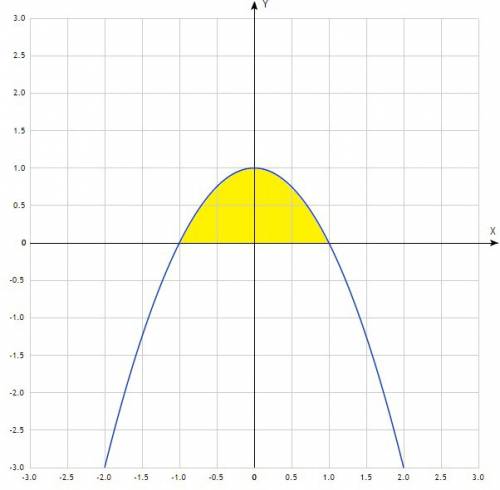
1250*400=500000 кв м
1 га = 100 м* 100м = 10000 кв м
значит поле 50 га