если число делится на 45, то оно также делится на 5 и на 9. если число делится на 5, то его последнюю цифра равна 0 или 5, а если число делится на 9, то и сумма его цифр тоже делится на 9. пусть наше число имеет вид abcd, тогда условие можно записать вот так:
первому неравенству, сумма цифр может иметь всего 4 значения: 9, 18, 27 и 36. так как , сумма не может быть равна 36. также d не может равняться 0, так как тогда бы произведение равнялось 0, а этого быть не может. значит,
если сумма равна 9, то произведение равно . тогда а остальные цифры принимают значения из набора 1, 1, 2.
если сумма равна 18, то произведение равно 19, что является простым числом, то есть его нельзя разложить на произведение чисел меньших 10.
если сумма равна 27, то произведение равно 5 не входит в разложение, противоречие.
итого имеем числа: 1125, 1215, 2115.
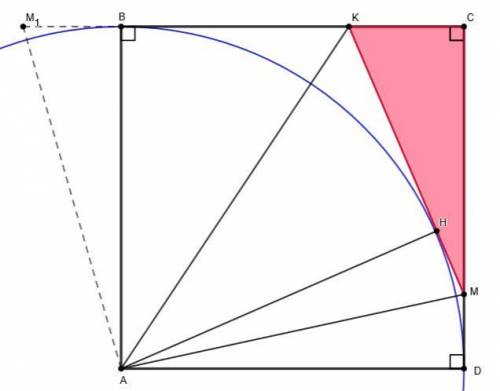
Условие: На сторонах ВС и CD квадрата ABCD взяли точки K и M так, что ∠MAK = 45°. Известно, что KM = 13 ,KC = 5 ,CM = 12. Найдите сторону квадрата ABCD.
Дано: K ∈ BC, M ∈ CD, ∠MAK = 45°, KM = 13 ,KC = 5 ,CM = 12.
Найти: BC.
Осуществим поворот ΔAMD на 90° против часовой стрелки ⇒ ΔAMD переходит в ΔAM₁B, ΔAMD = ΔAM₁B.
∠BAD = ∠BAK + ∠MAK + ∠MAD = 90° ⇒ ∠BAK + ∠MAD = 90° - ∠MAK = 90° - 45° = 45°
Из равенства ΔAMD = ΔAM₁B следует, что ∠MAD = ∠BAM₁, значит, ∠BAK + ∠BAM₁ = 45°.
ΔMAK = ΔM₁AK по двум сторонам и углу между ними:
AM = AM₁ - так как ΔAMD = ΔAM₁BАК - общая сторона∠MAK = ∠M₁AK = 45°Отсюда следует, что ∠АКМ = АКМ₁.
Аналогичным образом, осуществив поворот ΔAВК на 90° по часовой стрелке, можно утверждать, что ∠AMK = ∠AMD.
Заметим, что биссектрисы АК и АМ внешних углов при вершинах К и М ΔКСМ пересекаются в точке А, то есть точка А является центром вневписанной окружности ΔКСМ ⇒ AB = AD = AH - радиусы вневписанной окружности.
КВ = КН, MD = MH - как отрезки касательныхBC + СD = (BK + CK) + (CM + MD) = (KH + CK) + (CM + MH) = CK + CM + (KH + MH) = CK + CM + MK = 5 + 12 + 13 = 30
BC + СD = 30 ⇒ BC + BC = 30 ⇒ BC = 15
ответ: 15.