Центр вписанной в угол окружности лежит на биссектрисе. Окружности, вписанной в правильный многоугольник - в точке пересечения биссектрис его углов.
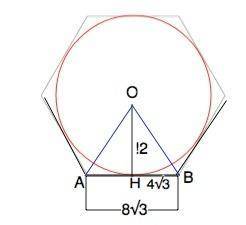
На рисунке приложения АВ - сторона, АО=ВО - биссектрисы углов правильного многоугольника. ОН - радиус вписанной окружности,
tg∠ОВН=ОН:ВН=√3. ⇒ Угол ОВН=60°, угол многоугольника 120°, смежный с ним внешний угол равен 60°.
Сумма внешних углов многоугольника 360°. Количество внешних углов, взятых по одному при вершинах, равно числу сторон многоугольника.
Число сторон 360°:60°=6.
Радиус описанной около правильного шестиугольника окружности равен его стороне.
R=8√3
C=2πR=16√3π
Пошаговое объяснение:
№154
78 : 3=26 см ширина
Площадь прямоугольника равна : S=a*b = 78 * 26= 2028 см²
Периметр равен: P=2(a+b)=2(78 +26) =208 см
№155
Площадь квадрата равна: S=a²=8²=64 смS=a*b =
№156
Площадь прямоугольника равна : S=a*b отсюда найдем длину другой стороны а=S/b= 192 : 16= 12 см
Периметр равен: P=2(a+b)=2(16+12)= 56 см
№ 158
Разобъем участок на два прямоугольника.
Найдем длину первого:
240 - 100= 140м длина
Площадь первого прямоугольника равна:
S1=a*b = 140 * 120= 16800м²
Площадь второго прямоугольника равна:
S2=a*b = 80 * 100= 8000 м²
Площадь всего участка : 16800 + 8000= 24800м²
600-200:у=20
400:у=20
у=400:20
у=20