и
и 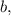 то ничего не изменится, всё будет работать как прежде.
то ничего не изменится, всё будет работать как прежде.
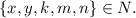
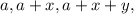 чтобы
чтобы![( [ a + 1 ] + x + y ) | ( 2a+x ) ,](/tpl/images/0497/6250/3dbb9.png)
![( [ a + 1 ] + x ) | ( 2a+x+y )](/tpl/images/0497/6250/bcfc5.png) и
и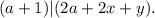
![k ( [ a + 1 ] + x + y ) = 2a + x](/tpl/images/0497/6250/3a31a.png) ;
;![(k-1) x + ky = 2a - k [ a + 1 ]](/tpl/images/0497/6250/d1c79.png) ;
;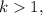 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.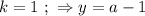 ;
;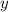 его значение
его значение 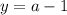 и будем искать такие комбинации
и будем искать такие комбинации 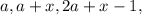 чтобы:
чтобы: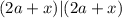 – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 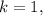
![( [ a + 1 ] + x ) | ( 3a+x-1 )](/tpl/images/0497/6250/b244e.png) и
и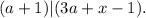
![m ( [ a + 1 ] + x ) = 3a+x-1](/tpl/images/0497/6250/c1228.png) ;
;![(m-1) x = 3a - 1 - m [ a + 1 ]](/tpl/images/0497/6250/be1b0.png) ;
;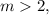 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.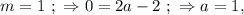 но это не подходит по условию.
но это не подходит по условию.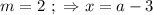 ;
; его значение
его значение 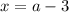 и будем искать такие комбинации
и будем искать такие комбинации 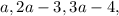 чтобы:
чтобы:![( 3 [ a - 1 ] ) | ( 3 [ a - 1 ] )](/tpl/images/0497/6250/de3e6.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 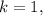
![( 2 [ a - 1 ] ) | ( 4 [ a - 1 ] )](/tpl/images/0497/6250/02549.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 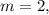
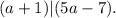
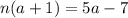 ;
;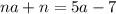 ;
; ;
;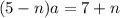 ;
;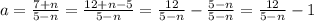 ;
;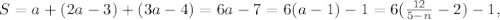
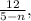 т.е. при
т.е. при 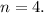
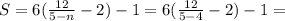
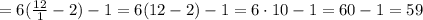 ;
;
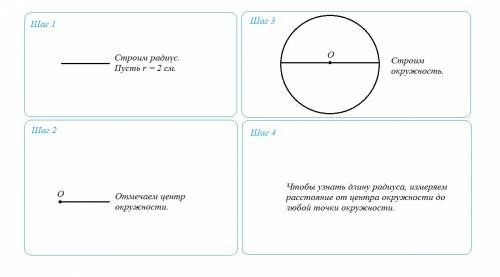
1) Строим отрезок, равный радиусу. Например, 2 см. То есть r = 2 см.
2) Отмечаем центр окружности (им будет край отрезка).
3) Измеряем циркулем отрезок, проводим окружность. Раствор циркуля должен оставаться неизменным.
4) Прикладываем линейку к радиусу и "продлеваем" его до пересечения с окружностью.
5) Чтобы узнать длину радиуса, нужно измерить расстояние от центра окружности до любой точки окружности.
упрощённый)
1) Берем произвольную длину радиуса. Пусть r = 2 см.
2) Так как радиус равен половине диаметра, то получаем следующее (вместо r подставляем значение радиуса):
d = 2r ⇒
d = 2·2 = 4 (см) - длина диаметра.
3) Отмечаем центр отрезка (диаметра). Это будет центр окружности.
Пусть O – центр окружности.
4) Строим окружность с центром в точке О.
5) Чтобы узнать длину радиуса, измеряем расстояние от центра окружности до любой точки окружности.