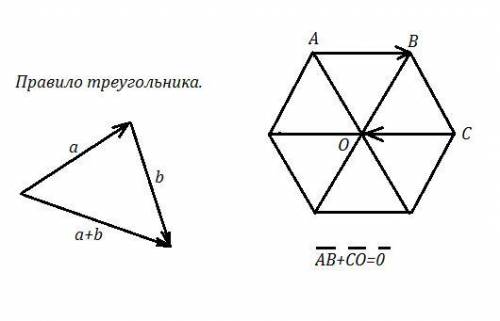
Правило треугольника сложения векторов. Если конец 1-го вектора совмещён с началом 2-го вектора, то суммой этих векторов будет вектор, начало которого совпадает с началом 1-го вектора, а конец - с концом 2-го вектора .
АВ+СО= 0 , так как при параллельном переносе вектора СО на линию, где лежит вектор АВ,совмещается начало вектора СО , точка С , с концом вектора АВ, точкой В, а конец вектора СО, точка О, совмещается с началом вектора АВ, точкой В. В таком положении вектор от точки А до точки О, совмещённой с точкой А, будет нулевой.
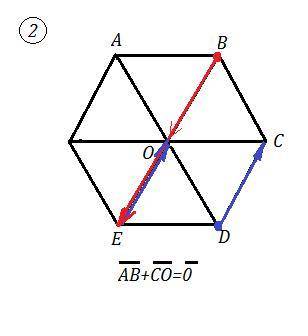
Теперь сложим 0+ВЕ=ВЕ.
ВЕ+DC=BO , так как при параллельном переносе вектора DC совмещаются точки D и Е , а также С и О . Фактически вычитается из вектора ВЕ его половина, остаётся вектор ВО.
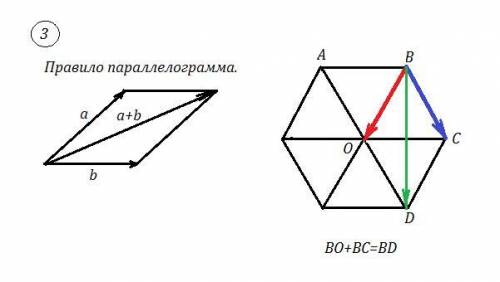
ВО+ВС=BD . Действуем по правилу параллелограмма. Если совмещены начала обоих векторов, то их суммой будет вектор, являющийся диагональю параллелограмма, построенного на этих векторах, причём диагональ выходит из общего начала.
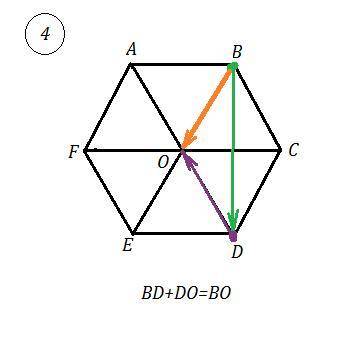
BD+DO=BO . По правилу треугольника у векторов-слагаемых совмещено начало вектора DO , точка D, с концом вектора BD, точка D. Поэтому результатом будет вектор ВО.
AB+CO+BE+DC+BC+DO=BO
1. Если число без остатка делится на 5, то оно заканчивается либо на 0, либо на 5. С остатком 2 - будет заканчиваться на 2 или 7.
2. Если число делится на 4 без остатка, то оно как минимум должно быть чётным. С остатком 2 чётность не меняется. А значит, заканчиваться число должно на чётную цифру. Из первого пункта нам подходит число, оканчивающееся на 2.
3. Если число без остатка делится на 3, то сумма цифр числа должна быть кратна 3.
Итак, имеем: 5Х2. Найдём Х, для этого используем условие из 3 пункта:
5Х2-2=5Х0. 5+Х+0 должно быть кратно 3, а значит вместо Х нам подходят только 1, 4, 7 (Х не более 9)
512: делится на 4 без остатка, не подходит.
542: подходит. Проверим:
542:3=180 (ост.2)
542:4=135 (ост. 2)
542:5=108 (ост. 2)
ответ: 542