15 м
Пошаговое объяснение:
.
Составим систему уравнений.
P ΔLBN = LB + BN + LN
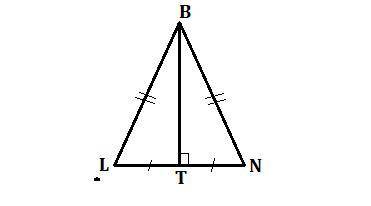
LB = BN, по свойству равнобедренного треугольника.
Пусть x м - LB и BN, тогда y м - LN
x + x + y = 50 - 1 уравнение
Составляем 2 уравнение:
P ΔLBT = LB + BT + LT
x м - LB
BT - высота, медиана, биссектриса (по свойству равнобедренного треугольника), значит LT = TN = 1/2LN
Тогда 1/2y м - LT
ΔLBT - прямоугольный, так как BT - высота
⇒ по теореме Пифагора:
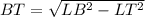
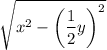м - BT
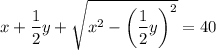- 2 уравнение
Решим получившуюся систему уравнений:
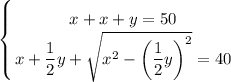
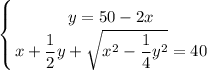
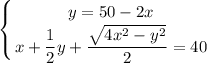
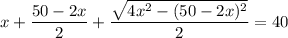
В числителе 2 дроби видим формулу сокращённого умножения - квадрат разности. Раскладываем по формуле: (a - b)² = a² - 2ab + b²
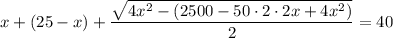
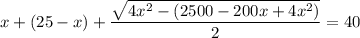
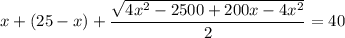
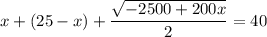
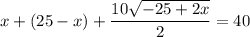
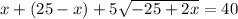
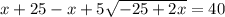
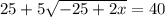
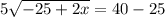
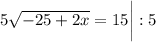
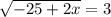
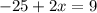
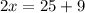
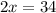
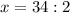
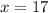
17 м - LB
17 + 17 + y = 50
y = 50 - 17 - 17
y = 50 - 34
y = 16
16 м - LN
LT = 1/2LN = 16/2 = 8 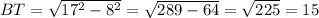м
м
.
P ΔLBN = LB + LN + BN
Так как ΔLBN - равнобедренный ⇒ LB = BN (по свойству равнобедренного треугольника)
⇒ P ΔLBN = 2LB + LN
2LB + LN = 50 м
P ΔLBT = LB + BT + LT
Так как BT - медиана, по условию ⇒ LT = 1/2LN
⇒ P ΔLBT = LB + BT + 1/2LN
LB + BT + 1/2LN = 40 м | · 2
2LB + 2BT + LN = 80 м
Так как 2LB + LN = 50 м ⇒ 2BT = 80 - 50 = 30 м
⇒ BT = 30 : 2 = 15 м
Пусть ширина окантовки х см, тогда ширина картинки с окантовкой равна (11 + х) см, длина - (33 + х) см, а площадь - (х + 11)(х + 33) см². Т.к. площадь по условию равна 779 см², то составим и решим уравнение
(11 + х)(33 + х) = 779,
363 + 11х + 33х + х² = 779,
х² + 44х + 363 = 779,
х² = 44х + 363 - 779 = 0,
х² + 44х - 416 = 0.
D = 44² - 4 · 1 · (-416) = 1936 + 1664 = 3600; √3600 = 60.
х₁ = (-44 - 60)/(2 · 1) < 0 - не подходит по условию задачи
x₂ = (-44 + 60)/(2 · 1) = 16/2 = 8
Значит, ширина окантовки равна 8 см.
ответ: 8 см.
