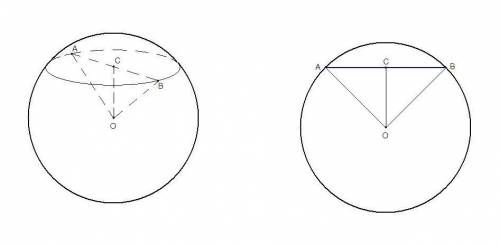
Сечение шара - круг. Пусть С - его центр, АВ - диаметр сечения.
ОС - отрезок, соединяющий центр шара с центром сечения, поэтому перпендикулярен сечению.
Тогда ВС - проекция радиуса ОВ на плоскость сечения.
Значит, ∠ОВС = 60° - угол между плоскостью сечения и радиусом шара.
ΔАОВ - равнобедренный (ОА = ОВ = R), значит
∠ОАС = ∠ОВС = 60°, тогда ∠АОВ = 60°.
AC = BC = AO/2 = 12/2 = 6 (По свойству прямоугольного треугольника: катет прилежащий углу 60° равен половине гипотенузы).
r = АС = АВ/2 = 6 см
S = πr² = π·6² = 36π см²
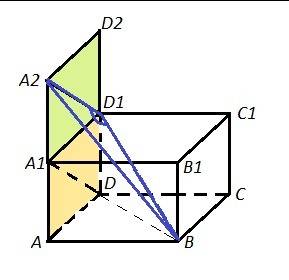
Задан куб с ребром а=1.
ВD1 - диагональ куба, DA1 - диагональ грани АА1D1D.
BD1 и DA1 - скрещивающиеся прямые.
Диагональ грани можно найти по теореме Пифагора:
DA1=√(AD²+AA1²)=√(1+1)=√2.
Диагональ куба можно найти , применив два раза теорему Пифагора:
ВD=√(AD²+AB²)=√2 , BD1=√(BD²+²DD1²)=√(2+1)=√3 .
Теперь проведём прямую D1A2║DA1 в плоскости AA1D. Мы как бы достроим пл. AA1D1D до пл. AA2D2D. Получили, что плоск. AA2D2D - прямоугольник, причём D1A2=DA1=√2.
Теперь можем соединить точки В и А2, т.к. они лежат в одной плоскости АВА2.
Рассмотрим ΔВА2D1. Угол BD1A2 будет искомым углом, т.к. угол между скрещивающимися прямыми можно найти как угол между прямыми, параллельными заданным скрещивающимся прямым.
Найдём ВА2 из ΔАВА2: ∠ВАА2=90° , АВ=1, А1А2=1+1=2 ( по построению).
ВА2=√(АВ²+АА2²)=√(1+4)=√5 .
Применим теорему косинусов для ΔВА2D1:
BA2²=D1A2²+BD1²-2·D1A2·BD1·cos∠BD1A2
5=2+3-2·√2·√3·cos∠BD1A2 ⇒ cos∠BD1A2=0 ⇒ ∠BD1A2=90°
1)360-120=240
2)240+140=380
2.
1)14+6=20
2)20:2=10
3)10+560=570.
3.
1)2*3=6
2)12-4=8
3)8+6=14