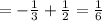1) Дан развёрнутый угол AOC. По свойству смежных углов, их сумма равна 180°. Вспомним, что градусная мера развёрнутого угла также равна 180°. Также, дан ∠BOC, градусная мера которого 65° (рассуждать можем несколькими но ответ получится один). Чтобы найти ∠AOB, надо из развёрнутого угла AOC вычесть все известные:
∠AOB = ∠AOC - ∠BOC = 180° - 65° = 115° - градусная мера ∠AOB
ответ: ∠AOB = 115°.
2) Дан прямой угол AOC, помним, что его градусная мера равна 90°, и дан ∠BOC, градусная мера которого равна 20°. Чтобы найти ∠AOB, надо из прямого угла AOC вычесть все известные (в нашем случае один):
∠AOB = ∠AOC - ∠BOC = 90° - 20° = 70° - градусная мера ∠AOB.
ответ: ∠AOB = 70°.
3) Дан развёрнутый угол COD (равен 180°), даны два угла: ∠AOC = 60°; ∠BOD = 50°. Чтобы найти ∠AOB, надо из развёрнутого угла AOC вычесть все известные:
∠AOB = ∠COD - ∠AOC - ∠BOD = 180° - 60° - 50° = 180° - (60° + 50°) = 180° - 110° = 70° - градусная мера ∠AOB.
ответ: ∠AOB = 70°.
Пошаговое объяснение:
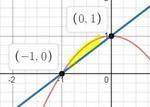
y₁= -x² + 1; y₂=x+1
строим график.
теперь пределы интегрирования как Вам понравится, так и считайте
а) по графтку х изменяется от -1 до 0
б) через уравнение у₁=у₂; -х²+1=х+1; -х² +1 -х -1=0; -х(х+1)=0; ⇒х₁ = -1; х₂=0
теперь формула.
здесь есть одна хитрость. чтобы не получить отрицательную площадь, (хотя это и не страшно, просто ответ дается без знака минус, но это как-то не прилично), так вот, чтобы не получить отрицательное значение интеграла, за у₁ принимается функция, которая на графике располагается "выше". у нас это у = -х² + 1
(y₁ - y₂) = -x² + 1- x-1= -x² - x =
и вот теперь площадь
