Есть такое правило разрядных единиц: при умножении десятичных дробей на десять/100/1000 (все, что без запятой и с ноликами) запятая уходит, а при делении влево. С разрядными единицами (0,1/0,01/0,00001) наоборот.
То есть, чтобы из десятичной дроби получить число с нулями без запятой нам сначала нужно избавиться от запятой.
При умножении на разрядную единицу уйдет столько цифр после запятой, сколько ноликов. Если мы умножим 0,75 на 10, то получим 7,5, а если на 100 - 75.
В числе 750000 четыре нуля, но нельзя забывать, что число 0,75 у нас запятой, если мы умножим на просто 10.000, то получим 7500, потому что два нолика мы потратили на освобождение от запятой. Значит, нам нужно число с шестью нулями, это будет 1.000.000, другими словами миллион. Именно умножив 0,75 на него мы получим 750000.
А теперь вернемся к другим разрядным единицам (0,1/0,0001..). Умножение и деление на них действует противоположно 10. То есть, если мы умножаем на 0.1, то запятая будет уходить не вправо, а влево. Но зато при делении запятая поползет куда надо. Правило с этой разрядной единицей таково: запятая настолько уйдет вправо или влево, сколько цифр находится после запятой. Если у нас есть 0.1 и мы умножаем на нее 4, то получим 0.4, потому что после нуля стоит одна цифра (единица), а если мы умножим 4 на 0.01, то получим уже 0.04.
Чтобы получить из 0.75 нужное число, нам надо делить на разрядную единицу 0.000001, ведь два нолика мы тратим на освобождение от запятой, причем ноликов всего пять, ведь шестой цифрой будет единица.
Значит, у этого примера есть два решения: 0.75 * 0.000001 = 750.000
и 0.75 * 1.000.000
3.1
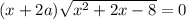
ОДЗ :
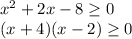
+ - +
-----------[-4]------------[2]---------------
x ∈ (-∞ ; -4] U [2 ; +∞)
Решим систему :
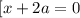
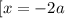
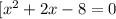
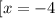
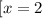
Уравнение будет иметь ровно два корня, если значение -2а не будет входить в ОДЗ или будет равняться значению -4 или 2. То есть если будет входить в промежуток [-4 ; 2]
Подставим конечные значение промежутка :
-2a = -4
a = 2
----------
-2a = 2
a = -1 - наименьшее значение
_________________________________
Уравнение будет иметь три корня, если значение -2а входит в ОДЗ и не равняется значению -4 и 2. То есть если будет входить в промежуток (-∞ ; -4) U (2 ; +∞).
Самое наименьшее натурально значение а, которое входит в данный промежуток, это а = 3
1. Наименьшее значение а, при котором уравнение имеет два корня: a = -1
2. Наименьшее натуральное значение а, при котором уравнение имеет три корня: a = 3
4.3
![(a^{2} -16)\sqrt[8]{x} = a+4](/tpl/images/1359/0078/fb245.png)
ОДЗ : x ≥ 0
Для начала рассмотрим 2 случая, когда а = 4 и а = -4
1. При а = 4 : 0 = 8 , x ∈ ∅
2. При а = -4 : 0 = 0, x ∈ [0 ; +∞)
Теперь мы можем поделить обе части уравнения на (a^2-16) :
![(a^{2} -16)\sqrt[8]{x} = a+4 | : a^{2} -16](/tpl/images/1359/0078/43567.png)
![\sqrt[8]{x} = \frac{a+4}{(a+4)(a-4)}](/tpl/images/1359/0078/af9ad.png)
![\sqrt[8]{x} = \frac{1}{a-4}](/tpl/images/1359/0078/22062.png)
Уравнение будет иметь корни, если правая часть будет больше или равно 0 :
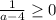
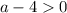
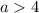
Уравнение будет иметь корни, если а ∈ (4 ; +∞) U {-4}
Наименьшее натуральное значение а, которое входит в данный промежуток, это а = 5
ответ : при а = 5
5/3x - 7 = 1/4
5/3x = 7 + 1/4
5/3x = 29/4
5x × 4 = 29×3
20x = 87
x = 87/20
x = 4,35