3) При возведении обеих частей уравнения в одинаковую четную степень не всегда получаются равносильные уравнения.
Пошаговое объяснение:
1) Утверждение не верно.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня. Например:
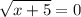
Это уравнение имеет корень х = -5!
2) Утверждение не верно.
Например, если возвести в нулевой степень (0 принадлежит множеству действительных чисел) уравнение, имеющий только корень х=0:
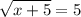
то получим
1 ≡ 1, что означает, последнее верно для любого х∈R.
3) Утверждение верно.
Уравнения называются равносильными, если имеют одно и то же множество корней.
В самом деле, рассмотрим иррациональное уравнение, которое не имеет корней:
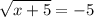
После возведения в квадрат получим:
x+5=25
А это уравнение имеет корень x=20!
а) Скорость автобуса возьмем за x км/ч,следовательно скорость машины x+27 км/ч
Автобус расстояние от города до поселка за 2 3/8 ч. Значит, S=u*t=x*2 3/8 км
Машина расстояние от города до поселка за 1 7/12 ч S=(x+27)*1 7/12 км
Уравниваем две получившиеся величины:
x*2 3/8=(x+27)*1 7/12 (раскрываем скобки в правой части)
2 3/8x=1 7/12x+27*19/12 (27*19/12=171/4=42 3/4)
2 3/8x-1 7/12x=42 3/4 *общий знаменатель 24
2 9/24x-1 14/24x=42 3/4
1 33/24x-1 14/24x=42 3/4
19/24x=42 3/4
19/24x=171/4
x=171/4 : 19/24=171/4*24/19=54 км/ч
Мы нашли скорость автобуса,находим расстояние по раннее выведенной формуле:S=u*t=x*2 3/8 км
54*2 3/8=54*19/8=1026/8=128,25 км
б)Скорость автобуса мы уже нашли -54 км/ч,скорость машины больше на 27 км/ч:54+27=81 км/ч
54/81*100%=2/3*100%=200/3%=66,6666...если округлить до второй цифры после запятой и получается 66,67%
в) Мы знаем,что скорость машины больше скорости автобуса на 27 км/ч
Отношение этой разницы к скорости автобуса умножаем на 100%
27/54*100%=0,5*100%=50%