logo
Вход Регистрация Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
Jek15
Jek15
05.09.2021 18:38 •  Математика

Из мешка в течении недели брали по 3 кг моркови каждый день, после чего в нём осталось 39 кг.на сколько дней хватило бы этого мешка моркови , еслибы каждый день из него брали по 7кг?

👇
Увидеть ответ
Ответ:
KsKitty
KsKitty
05.09.2021
1. 7•3=21 (кг) - это килограммы, которые брали в течении недели
2. 21+39=60 (кг) - было всего моркови
3. 60:7=8 дней
ответ: хватило бы на 8 дней.
4,4(53 оценок)
Открыть все ответы
Ответ:
maksimiksanov
maksimiksanov
05.09.2021

- 1 8 9 5 4 7 9                

1 5 8   2 3 9 . 9 2 4 0 5 0 6 3 2 9 1 1 3  79 × 2 = 158

- 3 1 5                    189 - 158 = 31

2 3 7                    79 × 3 = 237

- 7 8 4                   315 - 237 = 78

7 1 1                   79 × 9 = 711

- 7 3 0                  784 - 711 = 73

7 1 1                  79 × 9 = 711

- 1 9 0                 730 - 711 = 19

1 5 8                 79 × 2 = 158

- 3 2 0                190 - 158 = 32

3 1 6                79 × 4 = 316

- 4 0 0              320 - 316 = 4

3 9 5              79 × 5 = 395

- 5 0 0            400 - 395 = 5

4 7 4            79 × 6 = 474

- 2 6 0           500 - 474 = 26

2 3 7           79 × 3 = 237

- 2 3 0          260 - 237 = 23

1 5 8          79 × 2 = 158

- 7 2 0         230 - 158 = 72

7 1 1         79 × 9 = 711

- 9 0        720 - 711 = 9

7 9        79 × 1 = 79

- 1 1 0       90 - 79 = 11

7 9       79 × 1 = 79

- 3 1 0      110 - 79 = 31

2 3 7      79 × 3 = 237

7 3      310 - 237 = 73

Пошаговое объяснение:

4,5(88 оценок)
Ответ:
arpine1977
arpine1977
05.09.2021
1) Дифференциал функции у = f(x) равен произведению её производной на приращение независимой переменной х:

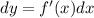dy = f '(x)dx или dy = y' dx

На практике достаточно найти производную и умножить её на dx. Дифференциал третьего порядка? Находим третью производную и умножаем на dx.

а) y = 3x^2-4x+5
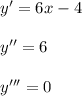
y' = 6x -4 \\ \\ y'' = 6 \\ \\ y''' = 0

dy = 0*dx =0

б) y = ln3x
y' = (ln3x)' = \frac{3}{3x} = \frac{1}{x} \\ \\ y'' = - \frac{1}{x^2} \\ \\ y''' = \frac{2}{x^3}

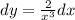
dy = \frac{2}{x^3} dx

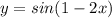
в) y = sin(1-2x)
y' = -2cos(1-2x) \\ \\ y'' = -4sin(1-2x) \\ \\ y''' = 8cos(1-2x)

dy = 8cos(1-2x)dx

2)
а) Просто подставляем х=3 и считаем:
\lim_{x \to \inft3} \frac{2x-6}{x^3+27} = \frac{2*3-6}{3^3+27} = \frac{0}{54}=0

б) Числитель и знаменатель делим на максимальную степень переменной икс, т.е. на x²:

\lim_{x \to \infty} \frac{3x^2-x-2}{x^2+x-1} = \lim_{x \to \infty} \frac{3- \frac{1}{x} - \frac{2}{x^2} }{1+ \frac{1}{x} - \frac{1}{x^2} } = \frac{3- \frac{1}{\infty}- \frac{2}{\infty^2} }{1+ \frac{1}{\infty}- \frac{1}{\infty^2} } = \frac{3-0-0}{1+0-0} = 3

в) Используем формулу синус двойного угла
\lim_{x \to \inft0} \frac{sin2x}{sinx} = \lim_{x \to \inft0} \frac{2sinxcosx}{sinx} = 2 \lim_{x \to \inft0} cosx =2*1 =2

г) используется сначала первый замечательный предел, а потом второй замечательный предел, вернее следствие из второго замечательного предела, а именно:
\lim_{x \to \inft0} \frac{e^x-1}{x} = 1

\lim_{x \to \inft0} \frac{e^x-1}{tgx} = \lim_{x \to \inft0} \frac{e^x-1}{ \frac{sinx}{cosx} } = \lim_{x \to \inft0} cosx \frac{e^x-1}{ sinx} = \\ \\ = \lim_{x \to \inft0} cosx * \lim_{n \to \inft0} \frac{e^x-1}{ sinx} = 1 * \lim_{x \to \inft0} \frac{ \frac{e^x-1}{x} }{ \frac{sinx}{x} } = \\ \\ = \frac{ \lim_{x \to \inft0}\frac{e^x-1}{x} }{ \lim_{x \to \inft0} \frac{sinx}{x} } =\frac{ \lim_{x \to \inft0}\frac{e^x-1}{x} }{ 1} = \lim_{x \to \inft0}\frac{e^x-1}{x} } = 1
4,5(90 оценок)
Это интересно:
К
Подробная инструкция: Как установить McAfee SiteAdvisor для Chrome...
Ф
Как избежать ошибок в дейтрейдинге...
Х
Как сделать кожаные браслеты своими руками: простые шаги для начинающих...
С
Как перестать быть ребенком в глазах родителей: советы психологов...
28.07.2020
Как справиться с гневом, связанным с видеоиграми...
З
Здоровье
09.02.2022
Как избежать повышенного кровяного давления: советы для здоровья...
С
Как выйти замуж в зале суда: подробное руководство...
Д
Дом-и-сад
11.12.2022
Как избавиться от скунсов: лучшие способы...
К
Как произвести расчет заработной платы в Excel...
З
Здоровье
25.10.2020
Как выпустить кровь из отекшей ушной раковины ( капустное ухо )...
Новые ответы от MOGZ: Математика
Meowmeowmi
Meowmeowmi
28.04.2022
[tex] {x}^{4} ={(3x - 4)}^{2} [/tex] решить уравнение. пробовал решить уже несколькими но что-то не получается ​...
marivtsan
marivtsan
17.05.2022
Объяснение решения и ,какой учебник посоветуете? ​...
таиса10
таиса10
25.06.2021
Известно,что a 0, b 0. сравните с нулём выражение -( a b) там ещё в конце a на верху 2...
LEST98
LEST98
07.04.2022
Розв яжіть рівняння х - 3,8 = 12,9...
Камила15111
Камила15111
19.03.2022
Знайти ймовірність того, що при підкиданні 3 гральних кубиків хоча б один раз випаде число 4.​...
ewenchester
ewenchester
29.12.2020
1/3x+5=16−1/6x 1/4y+8=19−1/12y 10x + 3 ( 7 - 2x ) = 13 +2x Решите уравнения...
melnikovao197
melnikovao197
28.01.2020
3.° 3Hargitu 3Ha4eHhl Bupa3y cos? 30° + sind 52° + cos2 52º.​...
катя7354
катя7354
31.01.2023
знайти площу бічної поверхні правильної трикутної призми, якщо ребро основи та діагональ бічної грані призми відповідно дорівнюють 5 і 13 см...
alik781
alik781
28.05.2023
10. Розв яжіть рівняння: а)(12,3-x) - 4,25 = 5,5; 6) 56,4- (2x - 3,86)=40,26...
Retrostyle
Retrostyle
24.05.2022
Сумма двх чисел равна 7 1/5 причем 1/3 большего числа равна меньшему числу. Найдите эти числа.​...

MOGZ ответил

Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ Оформи подписку
О НАС
ПОМОЩЬ
App
.
.
logo
Вход Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ