Математика: Сложение дробей с разными знаменателями

Сложение дробей с разными знаменателями

👇

Ответ:

eraly2

10.01.2022

Чтобы сложить дроби с разными знаменателями, необходимо сначала их привести к одному знаменателю. для этого надо найти наименьшее общее кратное для знаменателей обеих дробей, затем выполнить умножение числителей на дополнительные множители. только после этого возможно выполнить сложение числителей этих дробей при одном и том же знаменателе.

4,8(81 оценок)

Открыть все ответы

Ответ:

nicsiberia

10.01.2022

Наибольший общий делитель::

Разложим числа на простые множители и подчеркнем общие множители чисел:

15 = 3 · 5

18 = 2 · 3 · 3

Общие множители чисел: 3

НОД (15; 18) = 3

Наименьшее общее кратное::

Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем меньшее число. Подчеркнем в разложении меньшего числа множители, которые не вошли в разложение наибольшего числа.

18 = 2 · 3 · 3

15 = 3 · 5

Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:

НОК (15; 18) = 2 · 3 · 3 · 5 = 90

Наибольший общий делитель НОД (15; 18) = 3

Наименьшее общее кратное НОК (15; 18) = 90

Наибольший общий делитель::

Разложим числа на простые множители и подчеркнем общие множители чисел:

600 = 2 · 2 · 2 · 3 · 5 · 5

1075 = 5 · 5 · 43

Общие множители чисел: 5; 5

Чтобы найти НОД чисел, необходимо перемножить их общие множители:

НОД (600; 1075) = 5 · 5 = 25

Наименьшее общее кратное::

1075 = 5 · 5 · 43

600 = 2 · 2 · 2 · 3 · 5 · 5

НОК (600; 1075) = 5 · 5 · 43 · 2 · 2 · 2 · 3 = 25800

Наибольший общий делитель НОД (600; 1075) = 25

Наименьшее общее кратное НОК (600; 1075) = 25800

Пошаговое объяснение:

4,8(49 оценок)

Ответ:

JamesBond007007007

10.01.2022

x∈ (-n-2;-n+2]

Пошаговое объяснение:

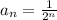
$a_n=\frac{1}{2^n}$

Вычислим радиус сходимости:

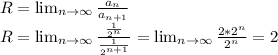
$R= \lim_{n \to \infty} \frac{a_n}{a_{n+1}}\\R= \lim_{n \to \infty} \frac{\frac{1}{2^n} }{\frac{1}{2^{n+1}} } = \lim_{n \to \infty} \frac{2*2^n}{2^n}=2$

Находим область сходимости степенного ряда:

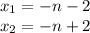
$x_1=-n-2\\x_2=-n+2\\$

x∈(-n-2; -n+2)

Остаётся проверить сходимость ряда на концах данного интервала.

При х = -n-2 мы получим следующий ряд:

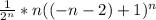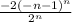
∑ $\frac{1}{2^n}*n((-n-2)+1)^n$ =∑ $\frac{-2(-n-1)^n}{2^n}$

Рассмотрим первых 3 члена данного ряда: -2; 1/8; -128

Данный ряд будем исследовать по признакам Лейбница

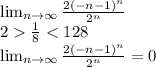
$\lim_{n \to \infty} \frac{2(-n-1)^n}{2^n} \\2\frac{1}{8}$

Как видим, выполняется лишь второе условие Лейбница, а значит ряд расходится => x=-n-2 является точкой расходимости.

Рассматриваем второй конец x=-n+2

Получаем следующий ряд

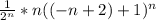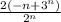
∑ $\frac{1}{2^n}*n((-n+2)+1)^n$ =∑ $\frac{2(-n+3^n)}{2^n}$

Тут исследуем по признакам Даламбера

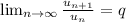
$\lim_{n \to \infty} \frac{u_{n+1}}{u_n}=q$

q=1 - неопределённость, т.к. при q>1 ряд расходится, а при q<1 - сходится.

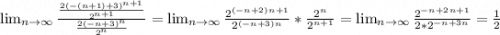
$\lim_{n \to \infty} \frac{\frac{2(-(n+1)+3)^{n+1}}{2^{n+1}} }{\frac{2(-n+3)^n}{2^n} }= \lim_{n \to \infty} \frac{2^{(-n+2)}^{n+1}}{2^{(-n+3)}^n} *\frac{2^n}{2^{n+1}}= \lim_{n \to \infty} \frac{2^{-n+2}^{n+1}}{2*2^{-n+3}^n} =\frac{1}{2}$