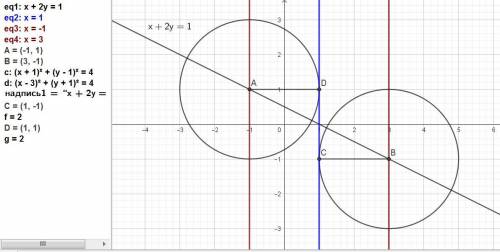
Так как не сказано, с какой стороны будет касание, то решений будет 2.
Так как заданная прямая, к которой будет касание, вертикальна, то центр окружности будет левее и правее её на величину радиуса, то есть появилось ещё одно условие расположения центра окружности.
Это будут прямые х = 1 - 2 = -1 и х = 1 + 2 = 3.
Находим координаты центров окружностей как точки пересечения заданной прямой x+2y-1=0 и двух найденных х = -1 и х = 3.
Подставляем значения х в уравнение прямой x+2y-1=0.
-1 + 2у -1 = 0,
2у = 2, у = 2/2 = 1.
Один центр найден: А(-1; 1).
Аналогично находим:
3 + 2у -1 = 0,
2у = -2, у = -2/2 = -1.
В(3; -1).
ответ: (x + 1)² + (y - 1)² = 2².
(x - 3)² + (y + 1)² = 2².
Признак делимости на 24. Число, делится на 24, если сумма всех цифр данного числа делится на 3, а число, образованное последними тремя цифрами данного числа делится на 8.
I Признак делимости на 16. Натуральное число делится без остатка на 16:
1) если последние четыре цифры в его записи образуют число, которое делится на 16;
2) если его запись оканчивается четырьмя нулями.
Для ясности признак делимости на 8 для однозначных и двузначных чисел не работает. Аналогично и для признака делимости на 16 такое же правило.
Очевидно, что число 72 делится на 24, так как сумма цифр 7+2=9 делится на 3 и делится оно на 8, но не делится на 16.
Возьмем к примеру число 120. Сумма цифр: 1+2+0 = 3 делится на 3 и три последние цифры числа 120 это 120 которое делится на 8. Значит число 120 делится на 24, но не делится на 16.
ответ: 72 или 120.