Пошаговое объяснение:
1) (4 1/9 ·3,3+126 13/30)·1,5÷60=(37/9 ·33/10 +126 13/30)·3/2 ·1/60=((37·11)/30 +3793/30)·1/40=(407+3793)/30 ·1/40=4200/(1200)=42/12=7/2=3,5
2) (2,07·4 4/9 -7,75)·80÷23,2=(207/100 ·40/9 -775/100)·80 ÷116/5=((23·40)/100 -775/100)·80·5/116=(920-775)/100 ·20·5/29=145/29=5
3) (36,3·7/11 +2,9)÷0,52·19=(363/10 ·7/11 +29/10) ÷52/100 ·19=(33·7+29)/10 ·1900/52=(231+29) ·190/52=260 ·95/26=10·95=950
4) (17 3/22 ÷29/66 -36,75)·60=(377/22 ·66/29 -36,75)·60=(13·3-36,75)·60=(39-36,75)·60=2,25·60=9/4 ·60=9·15=135
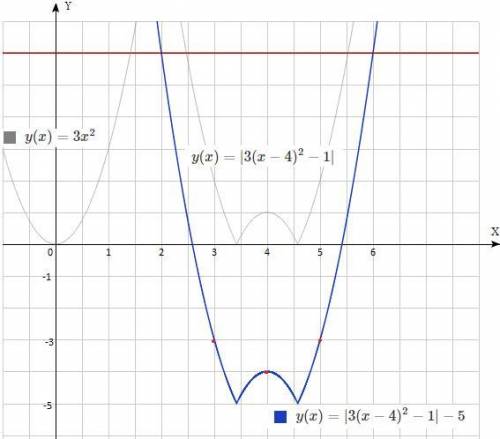
Найти сумму целых решений или решение неравенства |3(x-4)^2-1|-5<6
Пошаговое объяснение:
Построим два графика функций у=|3(x-4)²-1|-5 , у=6. Найдем все решения , которые лежат ниже прямой , из них выберем целые.
у=|3(x-4)²-1|-5 можно получить из параболы у=3х² преобразованиями
сдвиг у=3х² по ох на 4 вправо (у=3(x-4)²) ;сдвиг у=3(х-4)²по оу на 1 вниз (у=3(x-4)²-1);отображение части параболы относительно оси ох у=|3(x-4)²-1| ;сдвиг у=|3(x-4)²-1| на 5 вниз по оу (у=|3(x-4)²-1|-5).у=6 прямая .
Целыми решениями будут х=3,х=4,х=5. С умма равна 12