1) х+4 4/19=6 2/19
х = 6 2/19 - 4 4/19
х = 5 21/19 - 4 4/19
х = 1 17/19
2) х + 2х + х+7 = 39
4х = 39 - 7
4х = 32
х = 32 : 4
х = 8 (см) - одна сторона треугольника.
8 * 2 = 16 (см) - вторая сторона треугольника.
8 + 7 = 15 (см) - третья сторона прямоугольника.
3) Если площадь водохранилища Волгоградского обозначит за Х, то
Х + (Х+1463) + ( Х + 3383) = 14197
3Х = 14197 - 1463 - 3383
3Х = 9351
Х = 9351 : 3
Х = 3117 (км2) - площадь водохранилища Волгоградского.
3117 + 1463 = 4580 (км2) - площадь водохранилища Рыбинского.
3117 + 3383 = 6500 (км2) - площадь водохранилища Куйбышевского.
103 мандарина
Пошаговое объяснение:
Пусть x - кол-во мандаринов, а y - кол-во детей, тогда задаче соответствует следующая математическая модель (короче, составляем систему уравнений):
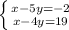
5y - кол-во мандаринов, отданных детям (каждому по 5), но тогда не хватит еще 2 мандарина, но фактически их нет (вот почему первое уравнение приравнивается к -2). Аналогично с 4y. Если детям отдали 4y мандаринов останется еще 19 мандаринов.
Остается решить систему уравнений.
1) Выразим x из первого уравнения:
x = 5y - 2
2) Подставим значение x во второе уравнение, тем самым получим простенькое линейное уравнение с одной переменной, и решим его:
5y - 2 - 4y = 19
y - 2 = 19
y = 21
3) Подставим значение y в выделенное уравнение (вообще, можно подставить в любое уравнение, но рациональнее в то, которое легче решается). В итоге имеем
x = 5 * 21 - 2
x = 105 - 2
x = 103
15 3/5 + 3 7/5=(15+3) + (3/5+7/5)= 18 + 10/5= 18 + 2=20