Найдите делимое, если: а)неполное частное 18, делитель 47, остаток 22; б) неполное частное 103, делитель 58, а остаток 33 в) неполное частное 0, делитель 65,а остаток 33.

👇

Увидеть ответ

Ответ:

hamzmxn66

03.07.2020

а) неполное частное 18, делитель 47,а остаток 22

Делимое 868

18·47+22=868

868:47=18 (ост.22)

б) неполное частное 103, делитель 58,а остаток 33

Делимое 6007

103·58+33=33

6007:58=103 (ост.33)

в) неполное частное 0, делитель 65,а остаток 33

Делимое 33

0·65+33=33

33:65=0 (ост.33)

4,4(4 оценок)

Открыть все ответы

Ответ:

rtgreezz

03.07.2020

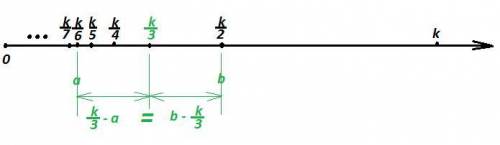
Расположим делители числа k в порядке возрастания (естественно, если такие делители существуют).

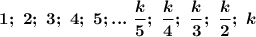
$\boldsymbol{1;~2;~3;~4;~5;...~\dfrac k5;~\dfrac k4;~\dfrac k3;~\dfrac k2;~k}$

Пусть a < b.

Так как различные натуральные делители a и b расположены на одинаковом расстоянии от числа k/3, то расположены они по разные стороны от числа k/3

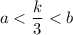
На числовой оси правее числа k/3 ( то есть больше числа k/3) расположены только два делителя : само число k и k/2.

b = k не подходит по условию, так как делитель a тогда отрицательный

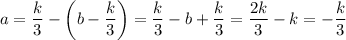
$a = \dfrac k3-\bigg(b-\dfrac k3\bigg)=\dfrac k3-b+\dfrac k3=\dfrac {2k}3-k=-\dfrac k3$

Остаётся единственный вариант 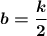$\boldsymbol{b=\dfrac k2}$

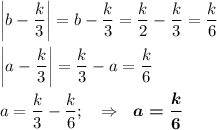
$\bigg|b-\dfrac k3\bigg|=b-\dfrac k3=\dfrac k2-\dfrac k3=\dfrac k6\\\\\bigg|a-\dfrac k3\bigg|=\dfrac k3-a=\dfrac k6\\\\a=\dfrac k3-\dfrac k6;~~\Rightarrow~~\boldsymbol{a=\dfrac k6}$

Так как у делителей 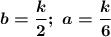$\boldsymbol{b=\dfrac k2;~a=\dfrac k6}$ общий знаменатель равен 6, то олимпиадными будут все числа, кратные 6. Тогда олимпиадных чисел, не превосходящих 2018:

2018 : 6 = 336,(3) - 336 чисел

Проверка :

k=6; b=3; a=1; |1-2|=|3-2| =1

k=12; b=6; a=2; |2-4|=|6-4| =2

k=18; b=9; a=3; |3-6|=|9-6| =3 ...

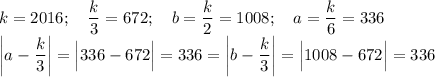
$k=2016;~~~\dfrac k3=672;~~~b=\dfrac k2=1008;~~~a=\dfrac k6=336\\\bigg|a-\dfrac k3\bigg|=\Big|336-672\Big|=336=\bigg|b-\dfrac k3\bigg|=\Big|1008-672\Big|=336$

ответ : 336 чисел

Назовём натуральное число k олимпиадным, если у него есть два раз- личных натуральных делителя a и b

4,8(46 оценок)

Ответ:

Mucuo31

03.07.2020

Проводник - это тело, внутри которого содержится достаточное количество свободных электрических зарядов перемещаться под действием электрического поля.
В проводниках возможно возникновение электрического тока под действием приложенного электрического поля.
Все металлы, растворы солей и кислот, влажная почва, тела людей и животных - хорошие проводники электрических зарядов.

Полупроводники́ — материалы, по удельной проводимости занимающие промежуточное место между проводниками и диэлектриками, и отличающиеся от проводников сильной зависимостью удельной проводимости от концентрации примесей, температуры и воздействия различных видов излучения. Основным свойством полупроводников является увеличение электрической проводимости с ростом температуры[1].

Полупроводниками являются кристаллические вещества, ширина запрещённой зоны которых составляет порядка электрон-вольта (эВ). Например, алмаз можно отнести к широкозонным полупроводникам (около 7 эВ), а арсенид индия — к узкозонным (0,35 эВ). К числу полупроводников относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк и другие), огромное количество сплавов и химических соединений (арсенид галлия и др.).

Изолятор ( или диэлектрик ) - тело не содержащее внутри свободные электрические заряды.
В изоляторах электрический ток невозможен.
К диэлектрикам можно отнести - стекло, пластик, резину, картон, воздух. тела изготовленные из диэлектриков называют изоляторами.
Абсолютно непроводящая жидкость – дистиллированная, т.е. очищенная вода,
(любая другая вода (водопроводная или морская) содержит какое-то количество примесей и является проводником).

4,5(2 оценок)

Это интересно:

Компьютеры-и-электроника

26.04.2020

Как изменить одежду сима в The Sims 2: простые шаги...

12.09.2020

Как остановить человека, который задирает вас...

Искусство-и-развлечения

07.05.2022

Как играть на тромбоне: советы и рекомендации для начинающих...

Кулинария-и-гостеприимство

25.08.2021