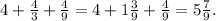1/6х-х+0.3х=1/5х+0,3х=1/5,3х
Если х=6,то 1/5,3*6=1/31,8=0,03144654088.Округлим до сотен=0,03
А8.2)12м 24 см
В3.7– 0,4 (6 + х) – 0,5 (4х - 3)=7-0,4*6+х-0,5*4х+3=7-0,4*6+х-4х*0,5+3=(7-0,4)*6+х-4х*(0,5+3)=6,6*6+х-4х*3,5=39,6+-3х*3,5=39,6+-10,5х.
Если х=10, то 39,6+-10,5*10=39,6+-105=-65,4
В4.1)90*0,4=36(градусов)40% прямого угла
2)180-36=144(градуса)разница
ответ:на 144 градуса.
В5.1)7,5/3=2,5(дней)
2)2,5*4,5=11,25(дней)
ответ:11,25 дней потребуется Лизе.
Прости, но дальше не могу.
∠M=45°
Пошаговое объяснение:
Определим угол в вершине треугольника MPK как угол между векторами MP и MK:
MP = OP - OM = (1; 4) - (-3 ;-2) = (1-(-3); 4-(-2)) = (4; 6)
MK = OK - OM = (2; -1) - (-3 ;-2) = (2-(-3); -1-(-2)) = (5; 1).
Скалярное произведение векторов MP(x₁; y₁) и MK(x₂; y₂) можно определить по формулам:
MP·MK=x₁·x₂+y₁·y₂ и MP·MK=|MP|·|MK|·cosα,
где |MP| и |MK| длины векторов MP и MK, α=∠M - угол между векторами MP и MK.
Определяем длину векторов MP и MK:
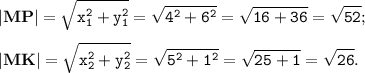
Скалярное произведение векторов MP(x₁; y₁) и MK(x₂; y₂) определяем через координаты:
MP·MK=4·5+6·1=26.
Тогда косинус угла между векторами MP и MK равен:
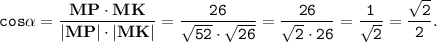
Так как
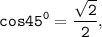
то ∠M=45°.
ответ: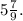
Сначала найдем эти первые три члена последовательности:
b₁ =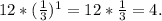
b₂ =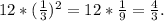
b₃ =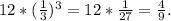
Теперь нужно сложить все получившееся числа:
b₁ + b₂ + b₃ =
=