Задача на логику
Вам нужно договориться, кто ВЫКЛЮЧАЕТ лампу
этот человек будет считать количество людей, побывавших в комнате с лампой
остальные же следуют следующей схеме:
если их впервые приводят в комнату, то они включают лампу, конечно же, если она не горит
в случае, если лампа горит, они ничего не делают и считают, что следующий их раз будет первым (т.е. первым будет именно тот раз, когда они придут и лампа будет выключена)
соответственно, каждый из пяти человек (кроме "выключателя") включит лампу ровно один раз
действия же выключателя просты:
если он заходит в комнату и видит включенную лампу, то он ее выключает и прибавляет к своему счетчику побывавших в комнате 1, если лампа выключена, то он ничего не делает
соответственно, когда у выключателя будут данные, что все 5 его друзей побывали в комнате (т.е. его счетчик будет равен 5), он может смело говорить, что все побывали в комнате.
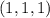 ,
, 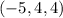 с точностью до перестановки.
с точностью до перестановки.
Пошаговое объяснение:
Из уравнения
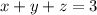
следует, что среди чисел 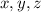 либо все нечетные, либо одно.
либо все нечетные, либо одно.
Заметим, что
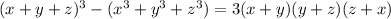
Из нашего условия это преобразуется как
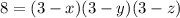
Но мы знаем, что среди чисел  либо все четные, либо одно. Если четны все, то они могут быть равны только
либо все четные, либо одно. Если четны все, то они могут быть равны только 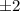 в этом случае числа
в этом случае числа 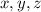 могут быть равны с точностью до перестановки только
могут быть равны с точностью до перестановки только 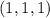 или
или 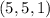 . Второе решение не подходит в исходное уравнение, поэтому его отметаем. Если же среди чисел
. Второе решение не подходит в исходное уравнение, поэтому его отметаем. Если же среди чисел  только одно четное, то оно обязано быть равно
только одно четное, то оно обязано быть равно 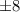 , а остальные -
, а остальные - 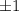 . В этом случае
. В этом случае 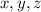 равны
равны 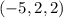 ,
, 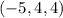 ,
, 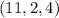 . Из этих троек нам подходит только вторая.
. Из этих троек нам подходит только вторая.
В итоге, решений всего два.