Проанализируем высказывания:
"Любой Бубут может рассуждать логически"- Это высказывание касается только Бубута и не распространяет свое действие на другие станные национальности)) НО следует что среди Бубутов нет тех, кто нелогичен
"Ни один Зюзют не может работать продавцом" - Т.е. все другие могут быть продавцами.
"Ни один из Чучут никогда не может рассуждать логически"- Значит ну нелогичная нация... остальных это не касается.
Теперь о выводах:
А) "если ты можешь рассуждать логически, то ты Бубут"
Вывод неверен, так как Зюзют тоже может рассуждать логически, (нелогичны только Чучуты)
Б) "если ты работаешь продавцом, то ты не Зюзют"
вывод верен- именно Зюзюты не могут быть продавцами
В) "Бубут не может работать продавцом"
Это почему? Продавцом не может быть только Зюзут, а Бубуты пусть работают) Значит вывод неверен.
Г) "Чучут может быть продавцом"
Про зависимость работы продавца и умение думать логически ничего не сказано. Значит пусть себе работает.. правда думать логически не может.. но это на работу не влияет. Вывод верен
Д) "если ты не рассуждаешь логически, то ты Чучут"
Хм... ну про Чучутов понятно- они не могут думать логически.. А как же быть с Зюзютом? Про них ничего не сказано. Так что и среди них найдутся те- кто не умеет думать логически. Вывод неверен
ДАНО: 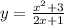
Исследование:
1. Область определения D(y). В знаменателе: 2*х+1 ≠0, х≠ - 0,5
Х∈(-∞;-0,5)∪(-0,5+∞) -
2, Непрерывность функции: разрыв при Х=-0,5.
Вертикальная асимптота: х = -0,5.
3. Проверка на чётность.
Y(-x) = (x²+3)/(-2*x+1) ≠ - Y(x) ≠ Y(x)
Функция ни чётная ни нечётная.
Вывод: нет ни осевой симметрии, как у функции y = x², ни центральной, как у функции y= x³
4. Пересечение с осью OХ. Y(x) = 0 - нет.
5. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X=(-oo;-0,5]
Положительная -Y(x)>0 X=[-0,5;+oo)
6. Пересечение с осью OY. Y(0) = 3.
7. Поиск экстремумов по первой производной.
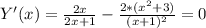
Корни Y'(x)= 0. Х4= 2x/2x = 1 Х5= ? (≈-2.25)
7. Локальные экстремумы.
Минимум Ymin(X4= 1) =4/3. Максимум Ymin(X5=8,36) = ?
8. Интервалы возрастания и убывания.
Возрастает Х=(-оо; x5]U[1;+oo) , убывает - Х=[x5;-0.5)∪(0.5;1]
9. Вторая производная
Корней производной - нет. Точка перегиба в точке разрыва при Х=-0,5
10. Выпуклая “горка» Х∈(-∞; -0,5)
Вогнутая – «ложка» Х∈(-0,5; +∞).
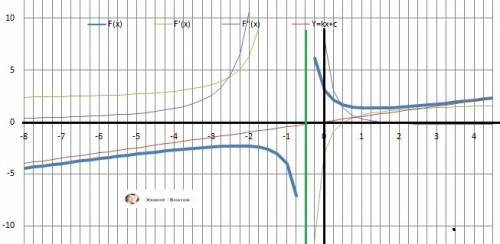
11. График в приложении.
5,4/1=5целых 2/5
5целых 2/5+5/13=5целых 51/65