D(f) ∈ (-∞;-1)∪(-1;+∞)
Пошаговое объяснение:
y=(X^2+4)/(X^3+1)
Первое,что мы должны проверить это наличие критической точки или так назваемой асимптотой,где функция не может существовать:
Знаменатель X^3+1 ≠ 0 ,потому-что на ноль числа делить нельзя,поэтому:
X^3+1 ≠ 0
X^3 ≠ -1
X≠-1
Это и есть та самая критическая точка!
Теперь так как данная функция дробно-рациональная,то эта функция схожа с функция 1/x ,то есть с гиперболой.
Функция 1/x может существовать в промежутка D(f)∈(-∞;0)∪(0;+∞) или D(f)∈R ,но при этом x≠0
Так как у нас данная функция y=(X^2+4)/(X^3+1) смещена,то и критическая точка смещается.
Поэтому область определения D(f) ∈ (-∞;-1)∪(-1;+∞) или D(f)∈R ,но при этом x≠ -1
Пошаговое объяснение:
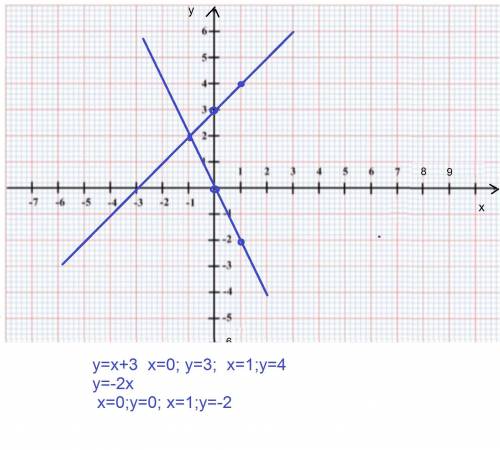
1)Решите графически систему уравнений.Выполните проверку,подставив найденные решения в уравнения системы :
графиком линейных функций являются прямые линии их можно построить по двум точкам
у=х+3 х=0; y=3; x=1;y=4
у=-2х x=0;y=0; x=1;y=-2
графики пересекаются в точке (-1;2)
проверка
-1+3=2
-1*(-2)=2 верно
2)Решите систему подстановки:
у=3-х
4х-у=12 4х-(3-х)=12; 4x-3+x=12; 5x=15; x=3; y=3-3=0; y=0
3) Не выполняя построений,найдите координаты точки пересечения графиков уравнений:
2х+3у=0
х-2у=28 умножим на -2
2х+3у=0
-2х+4у=56 сложим оба уравнения
7у=56; y=8; подставим в первое уравнение 2х+24=0 ;x=-12
(-12;8)