Пошаговое объяснение:
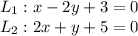
найдем точку пересечения прямых. для этого решим систему уравнений
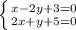
из первого выразим х х= 2у-3
подставим во второе 2(2у-3)+у+5=0; 4у -6 +у +5 =0; 5у=1; у=0,2
тогда х = 2*0,2 -3 = 0,4 -3 = -2,6
это наша точка пересечения М(-2,6; 0,2)
теперь уравнение прямой, параллельной оси оу
направляющий вектор оси оу s=(0;1), можем его использовать в качестве направляющего вектора искомой прямой, т.к. они параллельны
тогда каконическое уравнение прямой, проходяшей через точку М(-2,6; 0,2) параллельно оси оу будет
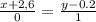
перейдем к обшему виду и получим
х = -2,6
1. 3√3
2.28°
Пошаговое объяснение:
1.
AOB центральный угол,равен дуге на которую опирается
дуга АВ=60°
угол АОВ=60°
рассмотрим треугольник АСО
угол АСО=90°
сумма всех углов треугольника 180°
угол САО=180°-90°-60°=30°
АО-гипотенуза прямоугольного треугольника АСО
АО=ВО (радиусы)
свойство угла 30° : катет лежащий против угла 30° равен половине гипотенузы
СО=АО/2
СО=6/2=3 (см)
по теореме Пифагора
АО^2=СО^2+АС^2
6^2=3^2+ АС^2
АС=√36-9
АС=√27=3√3
2.САВ вписанный угол,равен половине центрального угла,опирающегося на общую дугу
угол САВ 56°:2=28°