Предположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола () зеркально отобразится относительно оси (см. Рис. 1).
Рис. 1. Графики функций и
Таким образом, если у нас есть произвольный график , то для построения графика необходимо график симметрично отразить относительно оси (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси .
Рис. 2. Преобразование симметрии относительно оси
Преобразование симметрии – зеркальное отражение относительно прямой. График получается из графика функции преобразованием симметрии относительно оси .
На рисунке 3 показаны примеры симметрии относительно оси .
Рис. 3. Симметрия относительно оси Ox
49 см²
Пошаговое объяснение:
Вариант 1
Площадь прямоугольника - 14*7=98см²
Площадь прямоугольного треугольника считается по формуле =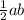 
где a и b - катеты.
Катеты треугольников ABS и CDU равны 7 и 7 см (точки S и U - середина, значит катеты CU и AS равны 7 см).
Отсюда площадь треугольника = 
= 24.5 см²
Площадь двух треугольников = 24.5*2=49 см²
Значит площадь заштрихованной фигуры = 98-49=49 см²
Вариант 2 (в качестве альтернативного решения)
т.к. точки U и S - середина, то образуются квадратыUCDS и BUSA со стороной 7 см. Т.к. треугольники занимают ровно половину квадратов, то получаем:
площадь квадрата - 7*7=49см²
из них заштрихованная = 49/2=24,5см²
Площадь двух заштрихованных областей - 24,5*2=49см²
58/18=
64/16=4 проверка 4*16=64
5/3=