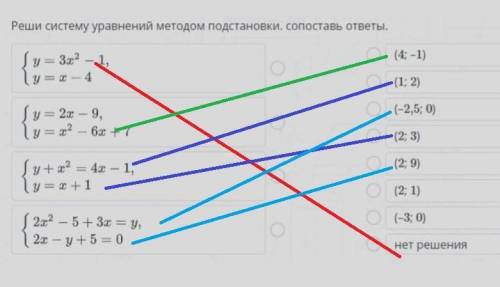
ответ: Смотрите соответствие на скриншоте.
Пошаговое объяснение:
1) у=3х²-1; (1)
у=х-4; (2)
---------
Из (2) у=х-4 подставим в (1):
х-4 = 3х²-1;
3х²-х + 3=0;
a=3; b=-1; c=3;
D= - 35<0 - нет решения.
***
2) у=2х-9; (1)
у=х²-6х+7; (2)
---------------------
Из (1) у=2х-9 подставим в (2)
2х-9 = х²-6х+7;
х²- 8х + 16 = 0;
По теореме Виета
х1+х2=8; х1*х2=16;
х=4;
Подставим в (1)
у=2*4-9=8-9;
у=-1.
***
3) у+х²=4х-1; (1)
у=х+1; (2)
---------------
Из (2) у =х+1 подставим в (1)
х+1+х² = 4х-1;
х²-3х + 2=0;
По теореме Виета:
х1+х2=3; х1*х2=2;
х1=2; х2=1;
---------
у1=2+1
у1=3;
-----------
у2=1+1;
у2=2.
***
2х² - 5 +3х = у; (1)
2х-у+5=0; (2)
--------------
Из (2) у=2х+5 подставим в (1)
2х²-5+3х=2х+5;
2х²+х-10=0;
a=2; b=1; c=-10;
D=b²-4ac=1² - 4*2*(-10) = 1+80 = 81>0 - 2 корня;
х1,2 = (-b±√D)/2a=(-1±√81)/2*2=(-1±9)/4;
x1= 2; x2= -2,5.
***
Подставим в (2)
у=2*2+5;
у1=9;
------------
у=2(-2,5)+5 = -5+5;
у2=0.
1) Вы, конечно, вначале найдёте первую производную по "х": [1/(3-2x)] ·[d(3-2x)/dx]+ 0,5·[d(x-7)/dx]
2) [1/(3-2x)] ·(-2) +0,5
3) 2/(2x-3)+0,5 ⇒ далее, приводя к общему знаменателю Вы получите
(2х+1)/(4x-6). Это искомая первая производная.
4) Далее, конечно, Вы приравняете производную к 0: (2х+1)/(4x-6)=0
Производная равна 0 при х= -0,5. Но как узнать, максимум это или минимум функции?
5)Для этого возьмите вторую производную, т.е производную от первой производной. Уверен, что получите следующее:(16х-16)/(4x-6)²
Это выражение и есть вторая производная. Она при значении х=-0,5 принимает значение∠0(т. отрицательное). А это и указывает на то, что при х=-0, 5 функция имеет максимум. Но какова величина максимума функции? ⇒ ln(3+1)+(-0,5-7)/2≈1,386-7,5≈ -6,114
УДАЧИ!
Пошаговое объяснение:
4/7=24, то 24:4*7=42
5%=35, то 35*100:5= 700
18%=36, то 36*100:18=200