Надеюсь, что я правильно помню
5. Смотрим на график на рисунке. Внимательно изучаем график. (За единицу взято две клеточки, а одна клеточка тогда 0,5).
а.) если х = 1, то у = 0,5;
б.) если х = -1, то у = -0,5;
в.) если х = 0,5, то у = 1;
г.) если х = -0,5, то у = -1;
6.
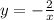
Что бы узнать принадлежит ли точка графику, нам нужно подставить числа в формулу. (В скобках на первом месте пишется "х", а на втором "у").
а.) А ( 1; -2)
Значит: х = 1, у = -2
Подставим "х" в формулу:
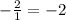
Видим, что у = -2. Точка А принадлежит графику.
(Дальше я буду использовать "/" как черту дроби).
б.) К ( -6; 1/3)
Значит: х = -6, у = 1/3
Подставим "х" в формулу:
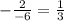
Видим, что у = 1/3. Точка К принадлежит графику.
в.) М (1/12; -6)
Значит: х = 1/12, у = -6
Подставим "х" в формулу:
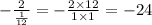
Видим, что у ≠ -24 (у = -6). Точка М не принадлежит графику.
г.) С ( -1; 1/2)
Значит: х = -1, у = 1/2
Подставим "х" в формулу:
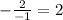
Видим, что у ≠ 2 (у = 1/2). Точка С не принадлежит графику.
7. Смотрим на график на рисунке.
а.) у = 1, х = -2
б.) у = -1, х = 2
в.) у = 2, х = -1
г.) у = -2, х = 1
13 задача
1)Найдём сколько % пути проехал поезд за 2 час:
6/6-30%
5/6-х%
х=(30*5)/6=25%
Тогда за 3ий час поезд проехал:
100%-(30%+25%)=45%
Найдём длину пути:
72 км-45%
х км-100%
45х=7200
х = 160 км
14 задача
2 любят музыку всех 3 стилей, уберем их пока.
Осталось 10 чел - рок, 13 -попсу, 8 - рэп.
3 любят рок и рэп, 5 рок и попсу, значит, 10-3-5=2 чела только рок.
5 любят рок и попсу, 4 попсу и рэп, значит, 13-5-4=4 только попсу.
3 любят рок и рэп, 4 попсу и рэп, значит, 8-3-4=1 только рэп.
Получилось:
2 любят все 3 стиля, 3 рок и рэп, 5 рок и попсу, 4 попсу и рэп.
2 любят только рок, 4 только попсу, 1 только рэп.
Всего 2+3+5+4+2+4+1=21
21 человек)
Пошаговое объяснение:
Выберем вершину большого куба и покрасим три ребра, исходящие из неё, в красный, зелёный и синий цвета. Теперь на каждом маленьком кубике напишем, сколько кубиков нужно пройти, двигаясь параллельно красному отрезку, сколько - параллельно синему отрезку и сколько - параллельно зелёному, чтобы в итоге оказаться в кубике, примыкающем к выбранной вершине (предполагается, что записано минимальные "расстояния"). Рассмотрим два чёрных кубика в одной "полоске". Чётности сумм их "расстояний" различны. Действительно, так как между ними чётное количество кубиков, то чтобы добраться от одного чёрного кубика до другого, придётся "пройти" нечётное число кубиков (считая тот, в который пришли). Теперь давайте выкрасим в белый цвет все кубики, сумма "расстояний" для которых нечётна. В каждой "полоске" был убран ровно один чёрный кубик, следовательно, ровно один чёрный кубик остался.