Пошаговое объяснение:
1) Берешь любые числа, которые подходят, чтобы при х-y = 8
это может быть, как я взяла х = 10, y = 2, может x = 9, тогда y = 1
и доп уравнение было бы x+y= 10
2) Оба уравнения должны быть одинаковыми, тогда и решение у них будет любое
потому что , если сократить 2х-2y = 16
2(x-y) = 16
x-y = 8, как и в условии
т.е ещё варианты: 3x-3y=24, 4x-4y=32 и т.д.
3) система не имеет решений тогда, когда два одинаковых уравнения равны разным числам
т.е. x-y = можно написать любое понравившееся число
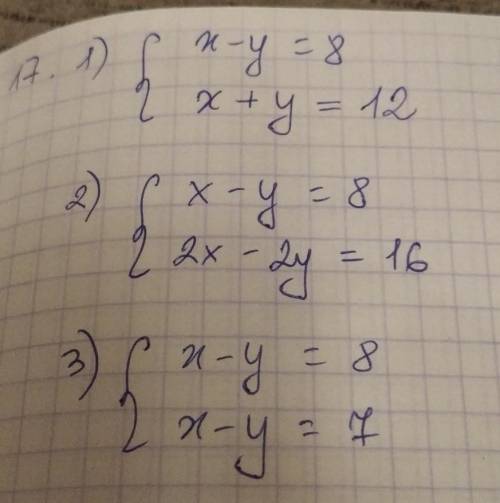
поскольку 4a<9, то a, которое удовлетворяет этому неравенству это 2(4*2 = 8<9). Ну и по смыслу второго неравенства вижу, что если a по-прежнему равно 2, то получается верное неравенство(3*2>4). Других вариантов у нас нет, так как данное число должно удовлетворять одновременно двум неравенствам. Значит, это число
2.
Либо же можно решить систему неравенств:
4a<9 a<2.25
3a>4 a>1+1/3
Находим разумеется пересечение решений этих неравенств, получаю промежуток:
(1+1/3;2.25). Но нас спрашивали в задаче про целые числа, значит a = 2 из этого промежутка 2 единственное целое число
Пошаговое объяснение:
по свойству квадратичной функции ее график касается оси ОХ если уравнение 3x^2-6x+k=0 имеет единственный корень, что имеет место быть в случае если дискриминант =0
b²-4ac=0
36-4*3*k=0
36-12k=0
12k=36
k=36/12
k=3