ответ:ответ. 102. Решение. Проведем отрезки BD и CE. Пусть они пересекаются в точке О. Заметим, что треугольники BCD и CDE равнобедренные с углом 108 при вершине, а значит, углы при основании равны 36 (они отмечены на рисунке одной дугой). Тогда BCE = BDE = 72. Угол COD равен 108 (т.к. в треугольнике COD два угла по 36). Поэтому COB = 180108 = 72. Углы по 72 отмечены на рисунке двумя дугами. Получаем, что треугольники CBO и DEO равнобедренные. Значит, AB = BO =BC = CD = DE = EO = х. Заметим, что OBA = 9636 = 60. Значит, треугольник OBA равнобедренный с углом 60 при вершине, т.е. равносторонний. Поэтому AO = x. Вычислим угол AOE AOE = EOBAOB = 10860 = 48. Треугольник AOE равнобедренный с углом 48 при вершине. Поэтому OEA = (18048)/2 = 66. Получаем, что угол E пятиугольника равен AED = AEO+OED = 66+36 = 10
Пошаговое объяснение:
Количество отрезков равно количеству комбинаторных сочетаний (ведь порядок вершин не важен) из 5 по 2:
(первое фото)
Чтобы обозначить все отрезки, можно использовать такой алгоритм. Сначала берём первую букву (самую левую) и объединяем с четырьмя оставшимися: PD, РМ, РТ, PS
Далее берём вторую букву слева. Сочетаем их только с буквами, стоящими справа, так как с первой буквой мы уже соединили в первом действии: DM, DT, TS. Третью букву: MТ, MS Четвёртую букву: TS.
В сумме получаем десять отрезков:(второе фото)
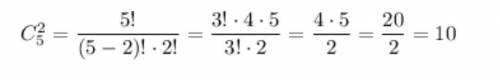
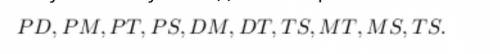
1-2
1-3
1-4
1-5
2-3
2-4
2-5
3-4
3-5
Ну ты понял и т.д. а потом посчитаешь