Пошаговое объяснение:
Доказать тавтологию - значит показать, что при всех истинностных значениях булевых переменных логическое выражение будет принимать только значение ИСТИНА.
Для первого логического выражения составляем таблицу (F - ЛОЖЬ, T - ИСТИНА):
![\left[\begin{array}{cccc}A&B&B\to A&A\to(B\to A)\\F&F&T&T\\F&T&F&T\\T&F&T&T\\T&T&T&T\end{array}\right]](/tpl/images/1511/7968/07c66.png)
Видно, что последний столбец, соответствующий заданному логическому выражению, состоит только из значений ИСТИНА при любом наборе булевых переменных.
Для второго логического выражения также составляем таблицу:
![\left[\begin{array}{ccccccccccc}A&B&C&A\to B&A\to C&(A\to B)\to (A\to C)&B\to C& A \to (B\to C)&Func\\F&F&F&T&T&T&T&T&T\\F&F&T&T&T&T&T&T&T\\F&T&F&T&T&T&F&T&T\\F&T&T&T&T&T&T&T&T\\T&F&F&F&F&T&T&T&T\\T&F&T&F&T&T&T&T&T\\T&T&F&T&F&F&F&F&T\\T&T&T&T&T&T&T&T&T\end{array}\right]](/tpl/images/1511/7968/ca9d4.png)
Видно, что последний столбец, соответствующий заданному логическому выражению, состоит только из значений ИСТИНА при любом наборе булевых переменных.
Таблица для третьего логического выражения:
![\left[\begin{array}{ccccccccccc}A&B&A\to B&\lnot A\to B&(\lnot A\to B)\to B&(A\to B)\to ((\lnot A\to B)\to B) \\F&F&T&F&T&T\\F&T&T&T&T&T\\T&F&F&T&F&T\\T&T&T&T&T&T\end{array}\right]](/tpl/images/1511/7968/0d62d.png)
Видно, что последний столбец, соответствующий заданному логическому выражению, состоит только из значений ИСТИНА при любом наборе булевых переменных.
То, что решается через характеристическое уравнение - это общее решение. Оно всегда будет независимо от правой части диффура.
По сути, нужно найти так называемое частное решение, и тогда решением для этого диффура будет сумма общего и частного решений.
Частное решение подбирается, исходя из правой части. В данном случае, правая часть есть многочлен второго порядка. Поэтому частное решение будет также иметь вид многочлена, причем многочлена второго порядка: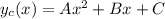 
(
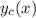- частное решение, A, B и C - константы, которые нужно подобрать). Теперь необходимо подставить это решение вместо y в данном диффуре, и найти константы.
(второго порядка потому, что многочлена первого порядка может не хватать, а многочлен не ниже третьего порядка избыточен, можешь попробовать подставить многочлен третьего порядка, но при нахождении коэффициентов он занулится)
UPD: ошибся в выборе многочена. Нужно использовать многочлен третьего порядка: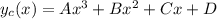 
(необходимо, чтобы после подстановки 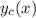в диффур в левой части получился многочлен не ниже порядка многочлена в правой части)
Для начала нам нужно узнать, сколько всего существует шестизначных чисел. Самое меньшее шестизначное - 100000, самое большее - 999999. Теперь вычтем из большего меньшее и прибавим 1 (потому что по сути мы считаем не сами числа, а промежутки между ними, это как про задачу с распиливанием бревна). Так вот, у нас получится, что всего шестизначных чисел - 900000.
Теперь будем считать те числа, где на первом и последнем местах стоит единичка. То есть у нас шесть позиций. На первом месте может стоять только одна цифра (наша единица), на втором месте может стоять что угодно, то есть 10 вариантов (0,1,2,3,4,5,6,7,8,9). На третьем, четвертом, пятом местах - аналогично, тоже 10 вариантов. На последнем, шестом месте, только один вариант (единичка). Эти числа нужно перемножить. То есть, 1*10*10*10*10*1 = 10^4
Теперь подсчитаем те числа, где на первом и последнем местах стоит двойка. Опять же, на первом месте может стоять только 2, то есть один вариант. На втором, третьем, четвертом, пятом местах - 10 вариантов. На последнем месте опять 1 вариант. Перемножим. Так же получим 10^4.
Теперь 10^4 умножим на 9 (цифр то 9 штук, а 0 не может стоять на 1 месте, а то получится пятизначное число). Будет 90000. Вот и ответ.
А вообще, Рахил, самому решать надо. Елисеев не оценит ;)