У дроби, где числитель и знаменатель меньше соответствующих в другой дроби, вид такой:
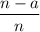
У другой дроби вид такой:
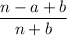
Вот теперь их сравним
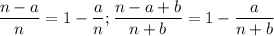
Для a, b и n имеется в виду, что это натуральные числа.
Получается, что фактически мы сравниваем
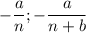
Если без минуса сравнивать их, то тогда дробь, где знаменатель больше, будет меньше (по аналогии делим пирог: на 3 части или на 7 частей, где на 7 частей, куски будут меньше).
А если с минусом, то тогда наоборот все, получаем, что
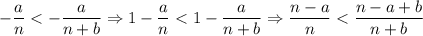
То есть больше будут дроби, где числитель со знаменателем больше.
В 1-ом случае у нас n=62, a=1, b=1 (вместо букв можно подставить эти числа и получить дроби из условия)
В 2-м случае у нас n=107, a=4, b=900
В 1-м случае получаем, что
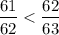
В 2-м случае получаем, что
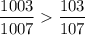
из первого взять одно кольцо
из второго взять два кольца
из третьего взять три кольца
из четвертого взять четыре кольца
Кольца и пакеты соответственно пометить, чтобы знать из какого пакета какие кольца. Всего взято (1+2+3+4=10 колец)
2. Взятые кольца взвесить. Кольца по 7г дают значения массы кратные 7, то есть 1×7=7, 2×7=14, 3×7=21, 4×7=28. По этим значения и определяют в каком пакете кольца по 7г. (Масса колец по 10г кратна 10).
Если после взвешивания получилась масса всех колец 88 г, то кольца по 7г в четвертом пакете (10+20+30+28=88)
Если после взвешивания получилась масса всех колец 91 г, то кольца по 7г в третьем пакете (10+20+21+40=91)
Если после взвешивания получилась масса всех колец 94 г, то кольца по 7г во втором пакете (10+14+30+40=94)
Если после взвешивания получилась масса всех колец 97 г, то кольца по 7г в первом пакете (7+20+30+40=97)