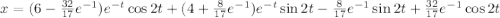Найдем сначала общее решение соответствующего однородного дифференциального уравнения:
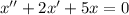
Используя замену 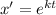 , получим характеристическое уравнение
, получим характеристическое уравнение
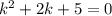
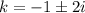
Общее решение однородного дифференциального уравнения:
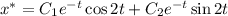
Рассмотрим функцию: 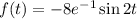 . Здесь
. Здесь 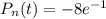 откуда
откуда 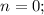 и
и 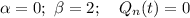 . Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
. Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
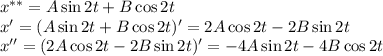
Подставляем в исходное дифференциальное уравнение:
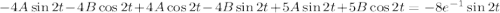
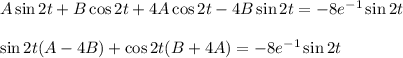
Приравниваем коэффициенты при cos2x и sin2x, получаем систему:
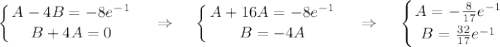
Общее решение линейного неоднородного дифференциального уравнения:
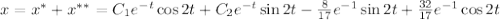
Осталось решить задачу Коши, подставляя начальные условия
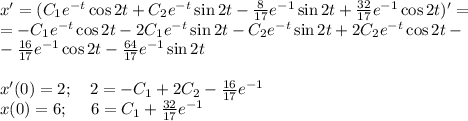
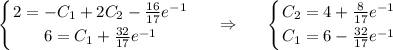
Частное решение задачки Коши:

Найдем сначала общее решение соответствующего однородного дифференциального уравнения:
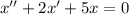
Используя замену 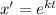 , получим характеристическое уравнение
, получим характеристическое уравнение
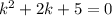
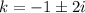
Общее решение однородного дифференциального уравнения:
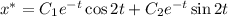
Рассмотрим функцию: 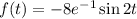 . Здесь
. Здесь 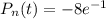 откуда
откуда 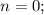 и
и 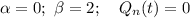 . Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
. Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
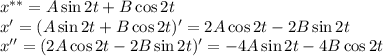
Подставляем в исходное дифференциальное уравнение:
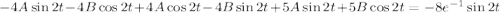
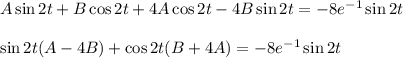
Приравниваем коэффициенты при cos2x и sin2x, получаем систему:
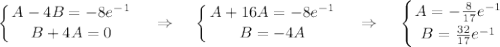
Общее решение линейного неоднородного дифференциального уравнения:
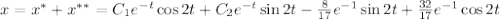
Осталось решить задачу Коши, подставляя начальные условия
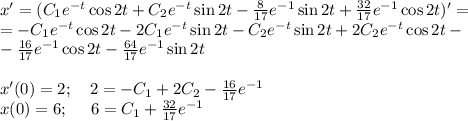
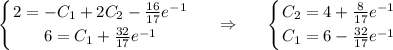
Частное решение задачки Коши: