Question

[умоляю! ]
[80] за решение система на фото!

Answer 1

Рассмотрим первое неравенство:

$25x^2+25y^2+100x+100y+56\leq 0\\25x^2+100x+100+25y^2+100y+100-144\leq 0\\25(x+2)^2+25(y+2)^2\leq 144\\(x+2)^2+(y+2)^2\leq (\frac{12}{5})^2$

Это круг с центром (-2; -2) и радиусом 2,4.

Рассмотрим второе неравенство:

$\sqrt{x^2+4x+4+y^2+10y+25}+\sqrt{x^2+12x+36+y^2+4y+4}\leq 5\\\sqrt{(x+2)^2+(y+5)^2}+\sqrt{(x+6)^2+(y+2)^2}\leq 0$

Первый корень — это расстояние от точки (-2; -5) до некоторой точки (x; y). Второй корень — это расстояние от точки (-6; -2) до этой же точки. Значит, левая часть — это сумма расстояний от точек (-2; -5) и (-6; -2) до некоторой точки. Минимальное такое расстояние — это расстояние между самими этими точками (то есть случай, когда точка лежит между известными точками) — равно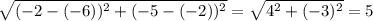 $\sqrt{(-2-(-6))^2+(-5-(-2))^2}=\sqrt{4^2+(-3)^2}=5$. Но по неравенству сумма расстояний не превосходит 5. Значит, оно равно 5 и задаёт множество точек, лежащих на отрезке, соединяющем точки (-2; -5) и (-6; -2) (то есть задаёт сам этот отрезок).

Найдём точки пересечения окружности и прямой, содержащей отрезок (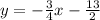$y=-\frac{3}{4}x-\frac{13}{2}$).

$(x+2)^2+(-\frac{3}{4}x-\frac{13}{2}+2)^2=\frac{144}{25}\\(x+2)^2+(\frac{3(x+6)}{4})^2=\frac{144}{25}\\x^2+4x+4+\frac{9x^2+108x+324}{16}-\frac{144}{25}=0|*400\\400x^2+1600x+1600+225x^2+2700x+8100-2304=0\\625x^2+4300x+7396=0\\(25x+86)^2=0\\x=-\frac{86}{25}=-3.44$

Решение ровно одно, значит, происходит касание. К тому же окружность касается именно отрезка, так как -6 < x < -2

$y=-\frac{3}{4}*(-\frac{86}{25})-\frac{13}{2}=-\frac{98}{25}=-3.92$

ответ: (-3,44; -3,92)