Эллипс.
Эллипс с каноническим уравнением
x2
a2
+
y2
b2
=1,a≥b>0, имеет форму изображенную на рисунке.
Параметры a и b называются полуосями эллипса (большой и малой соответственно). Точки A1(−a,0), A2(a,0), B1(0,−b), и B2(0,b), его вершинами. Оси симметрии Ox и Oy - главными осями а центр симметрии O− центром эллипса.
Точки F1(−c,0) и F2(c,0), где c=
√
a2−b2
≥0, называются фокусами эллипса векторы
¯
F1M
и
¯
F2M
− фокальными радиус-векторами, а числа r1=|
¯
F1M
| и r2=|
¯
F2M
|− фокальными радиусами точки M, принадлежащей эллипсу. В частном случае a=b фокусы F1 и F2 совпадают с центром, а каноническое уравнение имеет вид
x2
a2
+
y2
a2
=1, или x2+y2=a2, т.е. описывает окружность радиуса a с центром в начале координат.
Число e=
c
a
=
√
1−
b2
a2
(0≤e<1) называется эксцентриситетом эллипса и является мерой его "сплюснутости" (при e=0 эллипс является окружностью.)
Прямые D1:x=−a/e и D2:x=a/e, перпендикулярные главной оси и проходящей на расстоянии a/e от центра, называются директрисами эллипса.
Теорема. (Директориальное свойство эллипса)
Эллипс является множеством точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно e.
Примеры.
2.246. Построить эллипс 9x2+25y2=225. Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.
Пошаговое объяснение:
я не знаю правильно ли это
Пошаговое объяснение:
Для решения данной задачи требуется составить систему линейных уравнений. Пусть x - собственная скорость катера, а y - скорость течения.
Тогда получим следующее:
x + y - это будет скорость катера по течению.
x - y - это будет скорость катера против течения.
Имеем:

Раскрываем скобки:

Теперь уравняем переменные в системе:
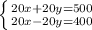
Уничтожаем 20y и -20y путем сложения.
Получаем:
40x = 900
x = 22,5 км/ч - собственная скорость. (Т.к. мы соб.скорость приняли за x)
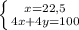



ответ: собственная скорость катера - 22,5 км/ч. А скорость течения - 2,5 км/ч
2) ( 78/150 ) + ( 28/150 ) = 106/150 = 53/75
3) ( 52/270 ) + ( 38/270 ) = 90/270 = 1/3
4) ( 157/270 ) - ( 97/270 ) = 60/270 = 2/9
5) ( 123/350 ) - ( 53/350 ) = 70/350 = 1/5
6) ( 39/350 ) + ( 11/350 ) = 50/350 = 1/7
7) ( 107/420 ) + ( 103/420 ) = 210/420 = 1/2
8) ( 287/420 ) - ( 117/420 ) = 170/420 = 17/42