1) Начало ряда кратных 15 чисел: 15, 30, 45, 60, ...;
2) На 6-м месте в этом ряду стоит число 15 * 6 = 90;
3) На 10-м месте: 15 * 10 = 150;
4) На 40-м: 15 * 40 = 600.
Пошаговое объяснение:
Числа, кратные 15 - это числа, делящиеся на 15 (и если мы считаем, что ряд таких чисел имеет начало, то чаще всего имеются ввиду положительные числа, удовлетворяющие данному требованию). То есть их можно представить в виде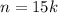 
, где n - произвольное число этого ряда, k - произвольное натуральное число. Первое число этого ряда, естественно, примет вид 15 * 1 = 15, а за ним пойдут все числа, большие него на 15m (m - некое натуральное число).
Тогда перед нами арифметическая прогрессия с первым членом 15 и разностью 15, и любой ее член можно вычислить по формуле 
, откуда и следуют все изложенные выше ответы.
1) Начало ряда кратных 15 чисел: 15, 30, 45, 60, ...;
2) На 6-м месте в этом ряду стоит число 15 * 6 = 90;
3) На 10-м месте: 15 * 10 = 150;
4) На 40-м: 15 * 40 = 600.
Пошаговое объяснение:
Числа, кратные 15 - это числа, делящиеся на 15 (и если мы считаем, что ряд таких чисел имеет начало, то чаще всего имеются ввиду положительные числа, удовлетворяющие данному требованию). То есть их можно представить в виде 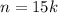, где n - произвольное число этого ряда, k - произвольное натуральное число. Первое число этого ряда, естественно, примет вид 15 * 1 = 15, а за ним пойдут все числа, большие него на 15m (m - некое натуральное число).
Тогда перед нами арифметическая прогрессия с первым членом 15 и разностью 15, и любой ее член можно вычислить по формуле , откуда и следуют все изложенные выше ответы.
знаем и что a²>0 , а² - положительное число
т.к. c< 0, с - отрицательное число
Умножение отрицательного и положительного числа мы получим отрицательное число.
Следовательно, ответ: Б) a²c <0