Слесарь за 2 смены вытачивает 6 деталей. сколько смен потребуется слесарю, чтобы выточить 30 деталей?

👇

Увидеть ответ

Ответ:

kristinashevku1

24.05.2022

30:6*2=10 смен ответ: 10 смен

4,5(19 оценок)

Ответ:

здрасти2003

24.05.2022

6/2=3детали за смену

30/3=10смен потребуется.

4,7(95 оценок)

Открыть все ответы

Ответ:

olik29

24.05.2022

Для того чтобы решить уравнение (неравенство) с модулем, надо рассмотреть все промежутки на которых при раскрытии модуля подмодульное выражение меняет знаки

В нашем уравнении два модуля.

Воспользуемся раскрытием модуля методом "коридора"

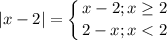
$\displaystyle |x-2|=\left \{ {{x-2; x\geq2 } \atop {2-x; x < 2 }} \right.$

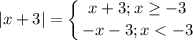
$\displaystyle |x+3| =\left \{ {{x+3; x\geq -3} \atop {-x-3; x< -3}} \right.$

тогда рисуем "коридор"

__(2-x)__-3 ___(2-x)__ 2 __(x-2)______

(-x-3) (x+3) (x+3)

теперь 1 промежуток x< -3

2-x+(-x-3)=14

2-x-x-3=14

-2x-1=14

-2x= 15

x= -15/2

x= - 7.5

т.к. -7.5 < -3 то корень подходит

теперь 2 промежуток -3 ≤x<2

2-x+x+3=14

5=14

на этом промежутке решений нет

теперь 3 промежуток x≥2

x-2+x+3=14

2x+1=14

2x=13

x=6.5

т.к. 6,5 >2 то корень подходит

ответ: -7,5 и 6.5

4,4(98 оценок)

Ответ:

makrona123

24.05.2022

1) Находим первую производную функции:
y' = -3x²+12x+36
Приравниваем ее к нулю:
-3x²+12x+36 = 0
x₁ = -2
x₂ = 6
Вычисляем значения функции на концах отрезка
f(-2) = -33
f(6) = 223
f(-3) = -20
f(3) = 142
ответ:   fmin = -33, fmax = 142
2)
a) 1. Находим интервалы возрастания и убывания.
Первая производная равна
f'(x) = - 6x+12
Находим нули функции. Для этого приравниваем производную к нулю
- 6x+12 = 0
Откуда:
x₁ = 2
(-∞ ;2)   f'(x) > 0   функция возрастает
(2; +∞) f'(x) < 0функция убывает
В окрестности точки x = 2 производная функции меняет знак с (+) на (-). Следовательно, точка x = 2 - точка максимума.
б) 1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = -12x2+12x
или
f'(x) = 12x(-x+1)
Находим нули функции. Для этого приравниваем производную к нулю
12x(-x+1) = 0
Откуда:
x1 = 0
x2 = 1
(-∞ ;0)   f'(x) < 0 функция убывает
(0; 1)   f'(x) > 0   функция возрастает
(1; +∞)   f'(x) < 0   функция убывает
В окрестности точки x = 0 производная функции меняет знак с (-) на (+). Следовательно, точка x = 0 - точка минимума. В окрестности точки x = 1 производная функции меняет знак с (+) на (-). Следовательно, точка x = 1 - точка максимума.

3. Исследуйте функцию с производной f(x)=2x^2-3x-1
1. D(y) = R
2. Чётность и не чётность:
f(-x) = 2(-x)² - 3*(-x) - 1 = 2x² + 3x - 1 функция поменяла знак частично. Значит она ни чётная ни нечётная
3. Найдём наименьшее и наибольшее значение функции
Находим первую производную функции:
y' = 4x-3
Приравниваем ее к нулю:
4x-3 = 0
x₁ = 3/4
Вычисляем значения функции
f(3/4) = -17/8
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y'' = 4
Вычисляем:
y''(3/4) = 4>0 - значит точка x = 3/4 точка минимума функции.
4. Найдём промежутки возрастания и убывания функции:
1. Находим интервалы возрастания и убывания.
Первая производная равна
f'(x) = 4x-3
Находим нули функции. Для этого приравниваем производную к нулю
4x-3 = 0
Откуда:
x₁ = 3/4
(-∞ ;3/4)   f'(x) < 0 функция убывает
(3/4; +∞)   f'(x) > 0   функция возрастает
В окрестности точки x = 3/4 производная функции меняет знак с (-) на (+). Следовательно, точка x = 3/4 - точка минимума

4,7(20 оценок)

Это интересно:

Образование-и-коммуникации

08.06.2023

Как найти площадь поверхности цилиндра: простой и понятный подход...

Компьютеры-и-электроника

26.11.2021

Как легко и быстро распечатывать с Samsung Galaxy Note 3...

Семейная-жизнь

21.02.2020

Как справиться с ребенком, который постоянно говорит нет...

02.01.2020