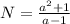ответ:
Пошаговое объяснение:
Из условия следует, что уравнение f(x)-x=0 не имеет решений. Поскольку f(x)-x - непрерывная функция, то она либо всюду положительна, либо всюду отрицательна, иначе она бы в некоторой точке принимала значение 0 (по теореме о промежуточном значении). Пусть f(x)-x всюду положительна. Это значит, что для любого x выполнено неравенство f(x)>x. Пусть f(x)=y. Тогда f(f(x))=f(y)>y=f(x)>x. Таким образом, при любом x f(f(x))-x>0, т.е. уравнение f(f(x))=x не имеет корней. Аналогичным образом, показываем, что уравнение f(f(x))=x не имеет корней и в том случае, когда для любого x выполнено неравенство f(x)<x.