Периметр прямоугольника 100см. чему равны длина и ширина если длина в 4 раза больше ширины? только без иксов решить

👇

Ответ:

tim4ik114

19.09.2020

Р=2(а+в)
где:
а - ширина
в - длина
по условию длина в 4 раза больше ширины, значит в=4а
теперь мы знаем:
ширина - а
длина - 4а
подставляем в формулу:
100=2(а+4а)
2(а+4а)=100
2а+8а=100
10а=100
а=100:10
а=10 - это у нас ширина
10*4=40 - это у нас длина
проверяем:
Р=2(40+10)
Р=2*50
Р=100
всё верно мы решилиЁЁЁ
ответ: длина = 40см, ширина=10см

4,7(34 оценок)

Открыть все ответы

Ответ:

qwdv

19.09.2020

Чтобы найти НОД чисел нужно разложить их на простые множители и перемножить между собой общие множители (подчёркнуты).

Чтобы сократить дробь, нужно числитель и знаменатель разделить на НОД.

1) 24 = 2 * 2 * 2 * 3

60 = 2 * 2 * 3 * 5

НОД (24; 60) = 2 * 2 * 3 = 12

$\tt\displaystyle\frac{24}{60}=\frac{24:12}{60:12}=\frac{2}{5}$

2) 45 = 3 * 3 * 5

105 = 3 * 5 * 7

НОД (45; 105) = 3 * 5 = 15

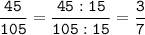
$\tt\displaystyle\frac{45}{105}=\frac{45:15}{105:15}=\frac{3}{7}$

3) 39 = 3 * 13

130 = 2 * 5 * 13

НОД (39; 130) = 13

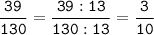
$\tt\displaystyle\frac{39}{130}=\frac{39:13}{130:13}=\frac{3}{10}$

4) 64 = 2 * 2 * 2 * 2 * 2 * 2

144 = 2 * 2 * 2 * 2 * 3 * 3

НОД (64; 144) = 2 * 2 * 2 * 2 = 16

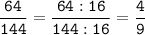
$\tt\displaystyle\frac{64}{144}=\frac{64:16}{144:16}=\frac{4}{9}$

===========================================================

Чтобы найти НОК чисел, нужно разложить их на простые множители и к множителям бОльшего числа добавить недостающие множители (подчёркнуты) и перемножить их между собой.

Наименьшее общее кратное и будет наименьшим общим знаменателем.

1) 12 = 2 * 2 * 3

8 = 2 * 2 * 2

НОК (12; 8) = 2 * 2 * 3 * 2 = 24

$\tt\displaystyle\frac{7}{12}=\frac{7*2}{12*2}=\frac{14}{24}$

$\tt\displaystyle\frac{5}{8}=\frac{5*3}{8*3}=\frac{15}{24}$

2) 9 = 3 * 3

15 = 3 * 5

НОК (9; 15) = 3 * 5 * 3 = 45

$\tt\displaystyle\frac{2}{9}=\frac{2*5}{9*5}=\frac{10}{45}$

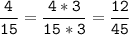
$\tt\displaystyle\frac{4}{15}=\frac{4*3}{15*3}=\frac{12}{45}$

3) 25 = 5 * 5

15 = 3 * 5

НОК (25; 15) = 5 * 5 * 3 = 75

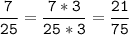
$\tt\displaystyle\frac{7}{25}=\frac{7*3}{25*3}=\frac{21}{75}$

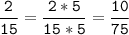
$\tt\displaystyle\frac{2}{15}=\frac{2*5}{15*5}=\frac{10}{75}$

4) 16 = 2 * 2 * 2 * 2

24 = 2 * 2 * 2 * 3

НОК (16; 24) = 2 * 2 * 2 * 3 * 2 = 48

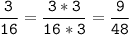
$\tt\displaystyle\frac{3}{16}=\frac{3*3}{16*3}=\frac{9}{48}$

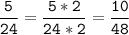
$\tt\displaystyle\frac{5}{24}=\frac{5*2}{24*2}=\frac{10}{48}$

4,5(32 оценок)

Ответ:

Ррррр5о

19.09.2020

Для нахождения точек максимума можно найти нули производной функции от функции момента волнения.

f'(x)=cos(4x)*[4x]'=4cos(4x).

4cos(4x)=0.

cos(4x)=0.

4x=Π/2+Πk, k-целое.

x=Π/8+2Πk/8.

На данном отрезке перебиру значения x чтобы найти экстремумы.

x=Π/8 k=0

x=3Π/8 k=1

x=5Π/8 k=2

x=7Π/8 k=3

x=9Π/8 k=4

x=11Π/8 k=5

x=13Π/8 k=6

x=15Π/8 k=7

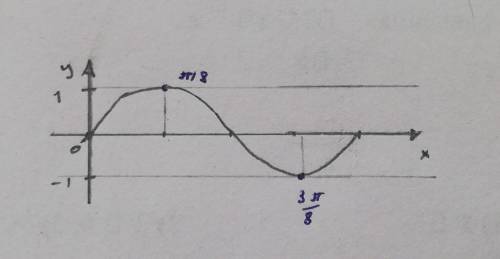
Схематически изображу часть графика функции y=sin(4x), определю, какие из точек экстремума точки максимума. Максимумы и минимумы чередуются у синусоиды, т.е. подходят

x=Π/8, x=5Π/8, x=9Π/8, x=13Π/8.

Итого 4 точки максимума.