Пошаговое объяснение:
1)объедини 2 прямые а и b в одну сверху 58 снизу х
итог прямая равна 180 х=180-58=122
2)на рисунке противолежащие углы равны
угол 1= угол 3=угол 4=угол 5
3) тоже что и 1
180-84=96
объяснение прямые c и d перпендикулярны b, а значит c||d
a-секущая которая проходит через эти прямые
4)периметр сумма всех сторон
СК объединяет середины сторон треугольника, является средней линией АС=2СК=13
В равнобедренном треугольнике высота это и медиана и биссектриса
АК=КВ
АК=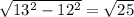 =5
=5
АВ=АК+КВ=5+5=10
АС=СВ=13
5) МНОГО заданий (но я не умею доказывать вроде 4-угольника может быть и квадратом и прямоугольником где две противоположные стороны попарно равны
Пошаговое объяснение:
1) |х-1,5|=4
х-1,5=4
х₁=5,5
х-1,5=-4
х₂=-2,5
2) |3-х|=5
3-х=5
х=3-5
х₁=-2
3-х=-5
х=3+5
х₂=8
3) |2х-3|=0
2х-3=0
2х=3
х=3/2
х=1,5
4) |6-5х|=0
6-5х=0
5х=6
х=6/5
х=1,2
5) |х+1|+5=3
|x+1|=3-5
|x+1|=-2 модуль не может быть отрицательным
Решений нет.
6) |х+5|-2=7
|x+5|=7+2
|x+5|=9
x+5=9
x=9-5
x₁=4
x+5=-9
x=-9-5
x₂=-14
7) |10х+6|=4
10x+6=4
10x=4-6
10x=-2
x₁=-0.2
10x+6=-4
10x=-4-6
10x=-10
x₂=-1
8) |1/m|=1/4
1/m=1/4
m₁=4
1/m=-1/4
m₂=-4
9) |3х-9|=6
3x-9=6
3x=15
x=15/3
x₁=5
3x-9=-6
3x=3
x₂=1
10) |5/m|=2/3
5/m=2/3
m=5*3/2
m₁=7.5
5/m=-2/3
m=-5*3/2
m₂=-7.5
11) |2,4x+1,2|=6
2.4x+1.2=6
2.4x=4.8
x=4.8/2.4
x₁=2
2.4x+1.2=-6
2.4x=-7.2
x₂=-3
12) |1/2n|=1/4
1/2n=1/4
n=1/4*2
n₁=1/2
1/2n=-1/4
n=-1/4*2
n=-1/2
{3x+y=7−5x+2y=3Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
{y=7—3x−5x+2(7−3x)=3Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
−5x+2(7−3x)=3⇒−5x+14−6x=3⇒⇒−11x=−11⇒x=1Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
y=7−3⋅1⇒y=4Пара (1;4) — решение системыСистемы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.Решение систем линейных уравнений сложенияРассмотрим еще один решения систем линейных уравнений сложения. При решении систем этим как и при решении подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.Последовательность действий при решении системы линейных уравнений сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.
Пример. Решим систему уравнений:
{2x+3y=−5x−3y=38В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
{3x=33x−3y=38Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение x−3y=38 получим уравнение с переменной y: 11−3y=38. Решим это уравнение:
−3y=27⇒y=−9Таким образом мы нашли решение системмы уравнений сложения: x=11;y=−9 или (11;−9)Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.