![\left[\begin{array}{ccc}3x&5y&7z\\2x&-1y&0?\\4x&3y&2z\end{array}\right]](/tpl/images/0826/6006/67d9d.png) (x, y, z написал для наглядности)..
(x, y, z написал для наглядности).. ![\left[\begin{array}{ccc}1\\2\\-1\end{array}\right]](/tpl/images/0826/6006/6a2b2.png)
![\left[\begin{array}{ccc}1&5&7\\2&-1&0\\-1&3&2\end{array}\right]](/tpl/images/0826/6006/88770.png)
![\left[\begin{array}{ccc}3&1&7\\2&2&0\\4&-1&2\end{array}\right]](/tpl/images/0826/6006/0df2a.png)
![\left[\begin{array}{ccc}3&5&1\\2&-1&2\\4&3&-1\end{array}\right]](/tpl/images/0826/6006/f8d8c.png)

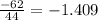
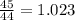
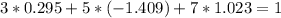
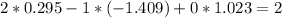
НОД (12; 20) = 4
НОД (27; 72) = 3 * 3 = 9
Пошаговое объяснение:
Наибольший общий делитель (НОД) двух чисел - это наибольшее число, на которое оба числа делятся без остатка.
1. НОД (12; 20)
Разложим на простые множители число 12 :
12 = 2 * 2 * 3
Разложим на простые множители число 20 :
20 = 2 * 2 * 5
Выберем одинаковые простые множители в обоих числах: 2, 2
Находим произведение одинаковых простых множителей и записываем ответ :
НОД (12; 20) = 2 * 2 = 4
2. НОД (27; 72)
Разложим на простые множители число 27 :
27 = 3 * 3 * 3
Разложим на простые множители число 72 :
72 = 2 * 2 * 2 * 3 * 3
Выберем одинаковые простые множители в обоих числах: 3, 3
Находим произведение одинаковых простых множителей и записываем ответ :
НОД (27; 72) = 3 * 3 = 9
cумма начальных цифр 1+9+9+6=25 - нечетное число
добавляя к двум числам 7, мы тем самим к общей сумме добавим 14(четное число), тем самым четность общей суммы не изменится, она останется нечетным
если мы могли бы получить четыре одинаковых числа за некоторое число ходов, то их общая сумма равна 4*одно из этих чисел, а значит была бы четным числом, что невозможно
следовательно из данных четырех чисел указанным получить четыре одинаковых числа невозможно