Тео́рия вероя́тностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними
Пошаговое объяснение:
Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Джероламо Кардано, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[2].Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
В XVIII веке важное значение для развития теории вероятностей имели работы Томаса Байеса, сформулировавшего и доказавшего Теорему Байеса.
В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Карл Гаусс детально исследовал нормальное распределение случайной величины (см. график выше), также называемое «распределением Гаусса».
Во второй половине XIX века значительный вклад внёс ряд европейских и русских учёных: П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова.
Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Пошаговое объяснение:
Определяем линии.
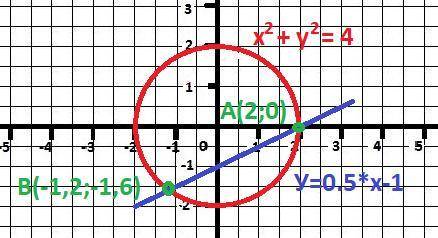
Это прямая линия и окружность радиусом R= √4 = 2
2*у = х-2 и у = 1/2*х - 1 - каноническая форму уравнения.
Рисунок к задаче в приложении.
Одна точка с явными координатами: А(2;0).
А для нахождения второй решим квадратное уравнение.
х = 2*y +2 - из уравнения прямой линии - подставим окружность.
(2*y +2)² + y² = 4
4*y² + 2*2*y*2 + 4 + y² = 4
5*y² + 8*y = 0 - квадратное уравнение - a*x² + b*x + c = 0
Вычисляем дискриминант - D.
D = b² - 4*a*c = 8² - 4*(3)*(0) = 64 - дискриминант. √D = 8.
Вычисляем корни уравнения.
у₁ = (-b+√D)/(2*a) = (-8+8)/(2*5) = 0/10 = 0 - первый корень
у₂ = (-b-√D)/(2*a) = (-8-8)/(2*5) = -16/10 = - 1,6 - второй корень
у1 = 0 и у2 = - 1,6 - координаты точек пересечения.
Вычисляем Х при У = - 1,6
х = 2*у + 2 = 2*(-1,6) + 2 = -1,2
В(-1,2;-1,6) - вторая точка пересечения - ответ.
900 человек - это 900/1200=0,75*100=75% - в аретли
100%-75%=25% - не в артели