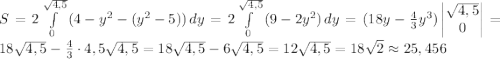Внимание!
В условии задачи опечатки. Одна исправлена, а вторая - нет. Запишем условие задачи правильно.
ДАНО:
1) y(x) = x+1 при х<1
2) y(x) = x² + 1 при - 1 ≤ х ≤ 1
3) y(x) = 3/(1 - x) при х > 1.
Пошаговое объяснение:
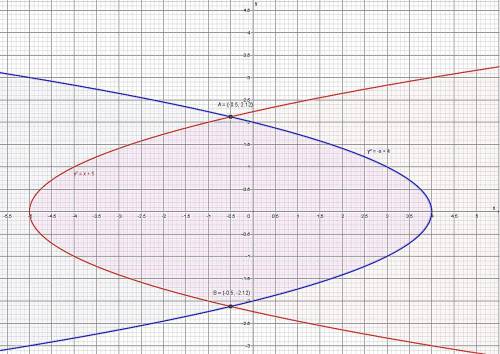
Три разных участка графика.
1) y = х +1 - прямая линия.
Построение по двум точкам, Например,
у= х + 1 = 0 получаем х = 1
х = -4 и у = -4+1 = - 3.
Важно! При Х=-1 функция не существует - точку (-1;0) изображаем в виде кольца ("дырки").
Область значений этой части функции - Е(у)∈(-∞;0)
2) y = x² + 1 - парабола поднятая на единицу вверх.
Для построения графика вычислим пять точек.
а) при х = 0 и у(0) = 1
б) при х= ±0.5 функция y= 1/4 + 1 = 1.25.
в) при х= ±1 функция у = 1 + 1 = 2.
Здесь по краям области определения она существует - ставим "точки", .
3) y = 3/(1-x) - гипербола.
Деление на 0 недопустимо. Находим область определения функции - D(y) ∈(1;+∞)
При x=1 - разрыв - вертикальная асимптота - к ней стремится линия графика.
Построение графика по нескольким точкам.
При х = 1. 1, у = 3/(-0,1) = - 30 (вне рисунка).
х = 1,5, у = 3/(-0,5) = -6.
х = 2, у = 3/(-1) = -3.
х = 3, у = - 1,5
х = 4, у = 3/(-3) = -1
х = 7, у = 3/(-6) = - 0,5
Соединяем точки плавной линией.
График функции на рисунке в приложении.
На графике видно, что имеются два разрыва.
Если точки в разрыве имеют конечные значения - это разрыв первого рода - при Х = -1. Он неустранимый, так как значения рядом с точкой х = -1 разные.
При Х = +1 - разрыв II рода - там нет значений справа от Х = 1.
Слева от х = 1 функция у = 2, а справа от х = 1 равна -∞.
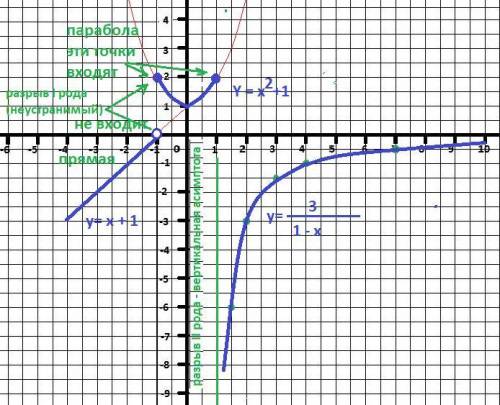
S = 18√2 ≈ 25,456
Пошаговое объяснение:
Построим параболы заданные уравнениями у² = x + 5, y² = -x + 4
Вершина параболы у² = x + 5 находится в точке (-5;0).
Ветви параболы у² = x + 5 направлены вдоль оси х по направлению возрастания.
Вершина параболы у² = -x + 4 находится в точке (4;0)
Ветви параболы у² = -x + 4 направлены вдоль оси х по направлению убывания.
Найдем точки пересечения двух парабол
Так как y² = y²
то x + 5 = -x + 4
2x = -1
x = -0,5
Находим значение y
y² = x + 5 = -0,5 + 5 = 4,5
y₁ = -√4,5 y₂ = √4,5
Получили две точки пересечения (-0,5;-√4,5) и (-0,5;-√4,5)
Чертеж рисунка во вложении
Интегрировать область пересечения лучше всего по у.
Тогда пределы интегрирования будут от y₁ = -√4,5 до y₂ = √4,5
Поскольку область интегрирования симметрична относительно оси у то умножим интеграл на 2 а пределы интегрирования изменим от y₁ = 0 до y₂ = √4,5
Область интегрирования сверху ограничена кривой х = 4 - y², а снизу ограничена кривой х = y² - 5