umkronchik95
умный
51 ответов
4.4 тыс. пользователей, получивших
первым вопросом мы должны найти бога, который не является богом случая, то есть является либо богом правды, либо богом лжи. Есть множество вопросов, которые могут быть заданы для достижения этой цели. Одна из стратегий — использование сложных логических связей в самом вопросе.
Вопрос Булоса: «Означает ли „da“ „да“, если и только если ты бог правды, а бог B — бог случая?». Другой вариант вопроса: «Является ли нечётным число истинных утверждений в следующем списке: ты — бог лжи, „ja“ означает „да“, B — бог случая?»
Решение задачи может быть упрощено, если использовать условные высказывания, противоречащие фактам (counterfactuals)[4][5]. Идея этого решения состоит в том, что на любой вопрос Q, требующий ответа «да» либо «нет», заданный богу правды или богу лжи:
Если я с тебя Q, ты ответишь «ja»?
ответом будет «ja», если верный ответ на вопрос Q это «да», и «da», если верный ответ «нет». Для доказательства этого можно рассмотреть восемь возможных вариантов, предложенных самим Булосом.
Предположим, что «ja» обозначает «да», а «da» обозначает «нет»:
Мы спрашивали у бога правды, и он ответил «ja». Поскольку он говорит правду и верный ответ на вопрос Q — «ja», оно обозначает «да».
Мы спрашивали у бога правды, и он ответил «da». Поскольку он говорит правду и верный ответ на вопрос Q — «da», оно обозначает «нет».
Мы спрашивали у бога лжи, и он ответил «ja». Поскольку он всегда лжёт, поэтому на вопрос Q он ответит «da». То есть правильный ответ на вопрос «ja», который обозначает «да».
Мы спрашивали у бога лжи, и он ответил «da». Поскольку он всегда лжёт, поэтому на вопрос Q он ответит «ja». То есть правильный ответ на вопрос «da», который обозначает «нет».
Предположим, что «ja» обозначает «нет», а «da» обозначает «да» , получим :
Мы спрашивали у бога правды, и он ответил «ja». Поскольку он говорит правду и верный ответ на вопрос Q — «da», оно обозначает «да».
Мы спрашивали у бога правды, и он ответил «da». Поскольку он говорит правду и верный ответ на вопрос Q — «ja», оно обозначает «нет».
Мы спрашивали у бога лжи, и он ответил «ja». Поскольку он всегда лжёт, поэтому на вопрос Q он отвечает «ja». Но, так как он лжёт, верный ответ на вопрос Q — «da», что означает «да».
Мы спрашивали у бога лжи, и он ответил «da». Поскольку он всегда лжёт, поэтому на вопрос Q он отвечает «da». Но, так как он лжёт, верный ответ на вопрос Q — «ja», что означает «нет».
Используя этот факт, можно задавать вопросы:[4]
Спросим бога B: «Если я с у тебя „Бог А — бог случая?“, ты ответишь „ja“?». Если бог B отвечает «ja», значит, либо он бог случая (и отвечает случайным образом), либо он не бог случая, а на самом деле бог A — бог случая. В любом варианте, бог C — это не бог случая. Если же B отвечает «da», то либо он бог случая (и отвечает случайным образом), либо B не бог случая, что означает, что бог А — тоже не бог случая. В любом варианте, бог A — это не бог случая.
Спросим у бога, который не является богом случая (по результатам предыдущего вопроса, либо A, либо C): «Если я с у тебя: „ты - бог лжи?“, ты ответишь „ja“?». Поскольку он не бог случая, ответ «da» обозначает, что он бог правды, а ответ «ja» обозначает, что он бог лжи.
Спросим у этого же бога «Если я у тебя с : „Бог B — бог случая?“, ответишь ли ты „ja“?». Если ответ «ja» — бог B является богом случая, если ответ «da», то бог, с которым ещё не говорили, является богом случая.
Оставшийся бог определяется методом исключения.
(см. объяснение)
Пошаговое объяснение:
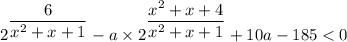
Рассмотрим внимательно данное неравенство.
Прежде всего обратим внимание на показатель второй двойки:
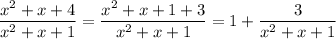
Тогда верна запись:
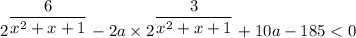
Сделаем замену вида 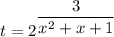 .
.
Получим неравенство:
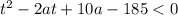
Переформулируем условие задачи:
Найти все значения параметра  , при каждом их которых записанное выше неравенство содержит промежуток
, при каждом их которых записанное выше неравенство содержит промежуток  .
.
Важным этапом решения будет заметить верхнюю границу для 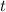 , так как с нижней вроде бы все ясно. Понятно, что для этого надо максимизировать
, так как с нижней вроде бы все ясно. Понятно, что для этого надо максимизировать  . В знаменателе дроби видим параболу, наименьшее значение которой достигается в вершине при
. В знаменателе дроби видим параболу, наименьшее значение которой достигается в вершине при 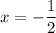 . Подставляя это значение в дробь получаем, что она примет значение
. Подставляя это значение в дробь получаем, что она примет значение 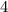 . Тогда
. Тогда 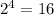 .
.
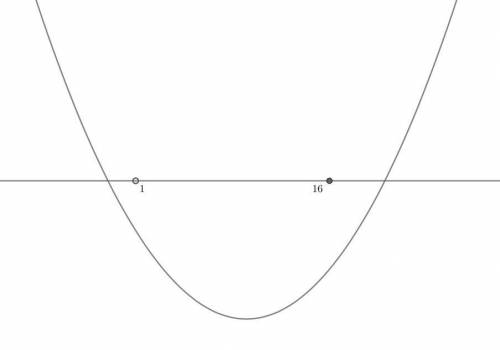
Введем функцию 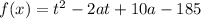 . Это парабола, ветви которой направлены вверх.
. Это парабола, ветви которой направлены вверх.
Выполним схематичный чертеж:
(см. прикрепленный файл)
Опишем полученное на языке математики:
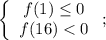
Тогда решить нужно:
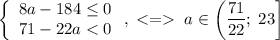
Итого при ![a\in\left(\dfrac{71}{22};\;23\right]](/tpl/images/2009/0489/8f843.png) исходное неравенство выполняется при всех
исходное неравенство выполняется при всех  .
.
Задание выполнено!
2 фермер- ?, в 5 раз меньше чем 1 фермеру
3 фермер- ?, в 6 раз меньше, чем 2 фермеру
Пусть кол-во ячменя у 3его фермера = x, тогда кол-во ячменя 2ого фермера = 6х, а кол-во ячменя у 1ого фермера будет = 5*6х, их сумма равна х+6х+(5*6х), а по условию задачи =1957 кг
Составим уравнение:
х+6х+5*6х=1957
37х=1957 | :37
х=
х=52
6х=52
30х= 52
ответ: ...