1) x²−7x−8 < 0
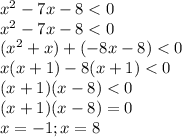
Определяем знаки на промежутках:
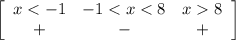
Интервал −1 < x < 8 — удовлетворяет неравенство
Точки выколотые, так как неравенство строгое, — их в ответ не вносим.
ответ: x ∈ (−1; 8).
2) 3x²−4x+7 ≥ 0
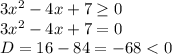
корней нет
делим обе части неравенства на 3х²−4х+7, 3х²−4х+7>0:
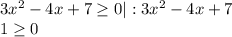
Неравенство выполняется, значит х ∈ R.
ответ: x ∈ (−∞; ∞).
3) x²−2x−3 > 0
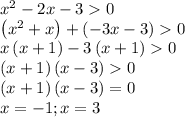
Определяем знаки на промежутках:
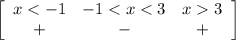
Интервалы x < −1 и x> 3 — удовлетворяют неравенство
Точки выколотые, так как неравенство строгое, — их в ответ не вносим.
ответ: x ∈ (−∞; −1) ∪ (3; +∞).
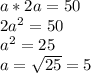Это в том случае, если оба числа положительные, тогда меньшее равно 5, большее 5*2=10, а их произведение 5*10=50. Однако, если числа отрицательные, то получается следующая картина: Рассмотрим отрицательные числа. Пусть теперь b-наибольшее число из двух, следовательно наименьшее будет 2*b. Их произведение равно 50. Решим уравнение : 
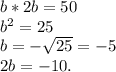Такие образом, получаем два ответа: когда числа положительные и когда отрицательные. В первом случае (пол.) наим. число 5, когда же числа отр. наименьшее число -10.
