Из двух пунктов, расстояние между которыми 75 км, одновременно в одном направлении выехали мотоциклист и велосипедист. Мотоциклист догонял велосипедиста со скоростью 30 км/ч. С какой скоростью двигался велосипедист, если мотоциклист догнал его через 5 ч?
Пусть х (км/ч) скорость велосипедиста, тогда скорость их сближения равна (30 - х) км/ч.
Зная, что встреча произошла через 5 ч, а изначальное расстояние между ними было 75 км, составим уравнение:
(30 - х) * 5 = 75
30 - х = 15
х = 30 - 15
х = 15
ответ: велосипедист двигался со скоростью 15 км/ч.
14,15 км/час
Пошаговое объяснение:
Пусть скорость катера будет х км/час, тогда его скорость по течению будет (х+3) км/час. Время по течению реки катер затратил 5/ (х+3) час, а по озеру 8/х час. Составим уравнение
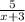 +
+ 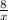 = 1
= 1
5x+8x+24=x(x+3)
12x+24=x²+3x
x²+3x-12x-24=0
x²-9x-24=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-9)² - 4·1·(-24) = 81 + 96 = 177
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = (9 - √177)/2·1 ≈ -2.1521 не корень
x2 = (9 + √177)/2·1 ≈ 11.152 корень
собственная скорость катера 11,15 км/час
по течению тогда
х+3=11,15+3=14,15 км/час
3000+450=3450