1) ∠КОМ=54°
∠КОМ+∠МOL=180° как смежные.
Тогда ∠МOL=180°-∠КОМ= 180°-54°=126°
∠LON - вертикальный к ∠КОМ, значит, ∠LON=∠КОМ=54°
ответ: 126°, 54°.
2) Прямые, что пересекаются, образуют четыре угла, попарно вертикальных. Пара углов, что не являются вертикальными, являются смежными и составляют развернутый угол (180°).
Поскольку сумма двух углов, что нам даны, не 180°, значит, это пара вертикальных углов.
92°:2=46° - величина двух образовавшихся углов.
Теперь найдем величину пары углов, что являются смежными к уже найденным.
180°-46°=134° - величина второй пары вертикальных углов.
ответ: 46°, 134°, 46°, 134°
3) PUR+RUT+TUQ=180°
PUR:RUT:TUQ как 1:3:5
Пускай ∠PUR=х, тогда ∠RUT=3х, а ∠TUQ=5х
х+3х+5х=180°
9х=180°
х=20°
Таким образом, ∠PUR=20°, ∠RUT=60°, ∠TUQ=100°
ответ: 20°, 60°, 100°
4
Пошаговое объяснение:
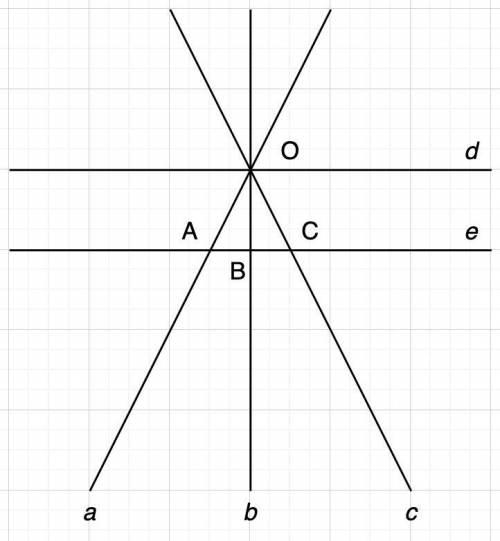
Обозначим исходные прямые как a, b и c, а их точку пересечения как O. Построим еще две прямые d и e так, что d проходит через O, а e параллельна d. Будем считать, что прямые a, b и c различны между собой. Также будем считать, что прямые d и e тоже различны.
Любые две прямые на плоскости либо не пересекаются, либо имеют единственную точку пересечения, либо совпадают. Если прямая d совпадает с одной из прямых a, b, c, то они имеют бесконечно много точек пересечения. Дальше будем рассматривать вариант, когда эти прямые различны.
Прямая e не проходит через точку O, иначе бы она совпадала с параллельной ей прямой d. Кроме того, прямая e не может быть параллельна ни одной из прямых a, b, c, поскольку в таком случае через точку O проходило бы две различных прямых, параллельных d.
Таким образом, прямые a и e пересекаются в точке A, прямые b и e -- в точке B, прямые c и e -- в точке C. Точки A, B и C различны между собой, поскольку они лежат на прямых a, b и c соответственно, а эти прямые уже проходят через одну общую точку O; иначе получилось бы, что через две точки проходит более одной прямой. Прямые d и e не пересекаются, потому что являются параллельными.
Итого получили четыре точки пересечения: O, A, B, C.
2)24*24=576 (см_2) - площадь