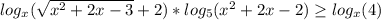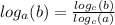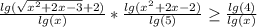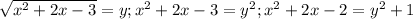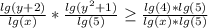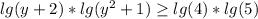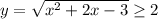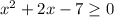С начало найдём площадь всего участка:
1) 47+12=59 (м) - одна сторона всего участка.
2) 58+25=83(м)- вторая сторона всего участка.
3) Sп = 83*59
Sп = 4,897 м2 - общая площадь участка.
Далее найдём площадь с подсолнухами:
4) Sп = 12*68
Sп = 816 м2 - площадь с подсолнухами.
Теперь площадь с капустой:
5) Sп = 25*12
Sп = 300 м2 - площадь с капустой.
площадь с помидорами мы найдём так:
6) Sп = 25*47
Sп = 1,175 м2 - площадь с помидорами.
Площадь с травой:
7) Sп = 58*42
Sп = 2,436
ответ: с помидорами=1.175 м2, с подсолнухами=816 м2, с капустой=300 м2, с травой=2.436 м2, общая площадь участка=4,897 м2второй вариант:(42+12)*(58+25)=4,897