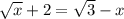 , то решение будет:
, то решение будет: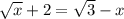 ;
;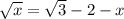 ;
;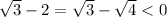 , значит при неотрицательных
, значит при неотрицательных  всегда выполняется
всегда выполняется 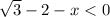 , что невозможно, занчит решений нет.
, что невозможно, занчит решений нет.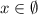 ;
;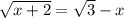 , то решение будет:
, то решение будет: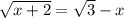 ;
;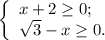 ;
;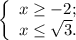 ;
;![x \in [ -2 , \sqrt{3} ]](/tpl/images/0480/7105/14c5f.png) ;
;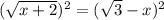 ;
;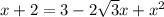 ;
;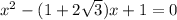 ;
;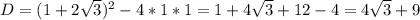 ;
;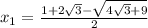 , решение входит в ОДЗ
, решение входит в ОДЗ , решение не входит в ОДЗ
, решение не входит в ОДЗ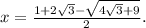
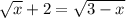 , то решение будет:
, то решение будет: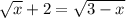 ;
;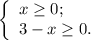 ;
;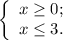 ;
;![x \in [ 0 , 3 ]](/tpl/images/0480/7105/e209c.png) ;
;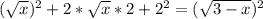 ;
;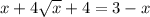 ;
;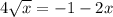 , что невозможно при неотрицательных значениях
, что невозможно при неотрицательных значениях  , занчит решений нет.
, занчит решений нет.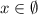 ;
;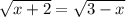 , то решение будет:
, то решение будет: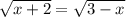 ;
;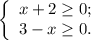 ;
;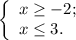 ;
;![x \in [ -2 , 3 ]](/tpl/images/0480/7105/248d4.png) ;
;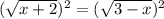 ;
;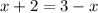 ;
;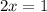 , что соответствует ОДЗ.
, что соответствует ОДЗ.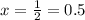 ;
;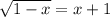 , то решение будет:
, то решение будет: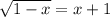 ;
;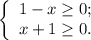 ;
;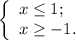 ;
;![x \in [ -1 , 1 ]](/tpl/images/0480/7105/5d24c.png) ;
;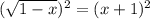 ;
;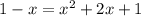 ;
;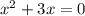 ;
;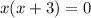 ;
;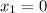 ;
; , что не соответствует ОДЗ.
, что не соответствует ОДЗ.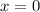 .
.
Ну логика решения у меня была такая:
составим уравнение с двумя неизвестными:
(1/3)x+(1/4)x+7+y=x где x- количество всех солдатиков, а y- количество желтых
приведем подобные и получим:
(5/12)x-7=y
Очевидно, что y - это натуральное число (как и x) , тогда нам нужно подобрать такое минимальное натуральное x, чтобы y был натуральным
Дальше идёт простой подбор, в результате которого мы выясним, что минимальный натуральный x, при котором y будет натуральным числом равен 24. Подставим 24 вместо x и получим, что y=3
Формулы, которыми мы будем пользоваться:
Длина окружности 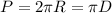
Площадь окружности 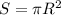
Пошаговое объяснение:
1.1 Утверждение неверное, так как отношение длины окружности к диаметру всегда равно Пи для всех окружностей (см. формулу длины окружности)
1.2 Да, утверждение верное, так как 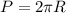 , и если мы умножим R на три, то и периметр или длина окружности так же увеличится в три раза
, и если мы умножим R на три, то и периметр или длина окружности так же увеличится в три раза
1.3 Данное утверждение неверно, т.к. зависимость площади круга от радиуса не линейна, а квадратична. То есть, если мы уменьшим радиус в два раза, то площадь уменьшится в 4 раза.
1.4 Верно, см. объяснение в 1.3
2. Воспользуемся формулой вычисления длины круга, приведённой вначале:

3. Воспользуемся формулой вычисления площади круга, приведённой вначале:
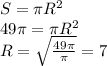
Пишем так
(х+2)^0.5 = (3-x)^0.5
Возводим в квадрат ОБЕ части уравнения и получаем.
x+2= 3-x
2x= 1
x=0.5
Второе запишем так
(1-x)^0.5 = x+1
1-x = x^2+2x+1
Упрощаем
X^2 + 3x = Х*(Х+3) = 0
Два корня X1=0 и Х2 = -3
Проверяем на ОДЗ - область допустимых значений - и видим. что корень уравнения Х2=-3 - не подходит. так как он ОТРИЦАТЕЛЬНЫЙ по знаку.
Подставляем - [1-(-3)]^0.5 = 4^0.5= + + 2 = -3+1= - - - 2 - не подходит.
Остается ОДИН корень = Х=0.