Найти общее решение дифференциального уравнения √ydx+x^2dy=0

👇

Ответ:

areg122004

28.03.2020

Это уравнение с разделяющимися переменными. Разделим его на произведение sqrt(y)*x*x, получим уравнение dx/(x*x)-dy/sqrt(y)=0, или
dx/(x*x)=dy/sqrt(y). Интегрируя обе части, получим 2*sqrt(y)=-1/x+C, откуда sqrt(y)=C/2-1/(2*x) = (C*x-1)/(2*x), а y =(C*C*x*x-2*C*x+1)/(4*x*x)

4,5(91 оценок)

Ответ:

luluik

28.03.2020

Решение дано в фотографии

Найти общее решение дифференциального уравнения √y*dx+x^2*dy=0

4,4(27 оценок)

Открыть все ответы

Ответ:

Рудиковичный

28.03.2020

1. Написать общее уравнение прямой, если прямая проходит через точку A(8;-4) и имеет направляющий вектор a(4;1).

Если известна некоторая точка , принадлежащая прямой, и направляющий вектор этой прямой, то уравнение данной прямой можно составить по формуле:

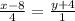
$\frac{x-8}{4} = \frac{y+4}{1}$

x-8 = 4y+16,

Получаем общее уравнение прямой: х-4у-24 = 0.

2. Написать общее уравнение прямой, если прямая проходит через точку N(-2;6) и имеет угловой коэффициент k=2.

Уравнение с коэффициентом: у = ах+в.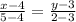
Подставим координаты точки N: 6 = 2*(-2) + в, отсюда находим значение в: в = 6+4 = 10.
у = 2х + 10.
Уравнение общего вида: 2х-у+10 = 0.
3. Написать общее уравнение прямой, если прямая проходит через точки K(4;3) и B(5;2).
$\frac{x-4}{5-4}= \frac{y-3}{2-3}$
-1(x-4) = 1(y-3),
-x+4 = y-3,
x+y-7 = 0.
4. Написать общее уравнение прямой, если прямая проходит через точку M(-2;4) и имеет нормальный вектор n(6;2).
В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Составим при А = 6 и В = 2 уравнение прямой: 6х + 2у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки М.
6*(-2)+2*4+С = 0. Отсюда С = 12-8 = 4.
Получаем уравнение: 6х + 2у + 4 = 0.
5. Определить координаты направляющего вектора прямой x-1/12=y+2/-4.
Это числа в знаменателях канонического уравнения прямой:
р(12;-4).
6. Найти угловой коэффициент прямой 6x+3y-13=0.
Для этого заданное общее уравнение преобразовать в уравнение с коэффициентом: 6x+3y-13 = 0.
3y = -6x + 13.
у = -2х +(13/3).
Угловой коэффициент прямой равен -2.

4,5(15 оценок)

Ответ:

misterpordon

28.03.2020

Деревья, формирующие лес, растут более или менее сближенно, оказывая влияние друг на друга и на всю остальную лесную растительность. Растения в лесу расположены ярусами, которые можно сравнить с этажами. Верхний, первый ярус представлен основными деревьями первой степени значимости (ель, сосна, дуб). Второй ярус сформирован деревьями второй величины (черемуха, рябина, яблоня). Третий ярус состоит из кустарников, например, шиповника, лещины, калины, бересклета. Четвертый ярус – это травянистый покров, а пятый – мхи и лишайники. Доступ света к растениям различных ярусов неодинаков. Кроны деревьев первого яруса лучше освещены. От верхних к нижним ярусам освещенность уменьшается, так как растения верхних ярусов задерживают долю солнечных лучей. Мхи и лишайники, занимающие пятый ярус, получают очень малое количество света. Это самые теневыносливые растения леса.
Разные леса имеют различное количество ярусов. К примеру, в темном еловом лесу различимы только два-три яруса. На первом ярусе расположены основные деревья (ели), на втором – небольшое число травянистых растений, а третий образован мхами. Другие древесные и кустарниковые растения не растут во втором ярусе елового леса, так как не выносят сильного затенения. Также не наблюдается в еловом лесу и травянистый покров.

4,8(79 оценок)

Это интересно:

Образование

06.01.2021

Клюква стоит 250 рублей за кг, а малина 200....

Образование

16.03.2023

Решить систему уравнений x2 + y2 + xy = 3...

Образование

05.08.2020

Решить систему уравнений x2 + xy +y2 = 13...

Образование