90 книг на первой полке
42 книги на второй полке
84 книги на третьей полке
Пошаговое объяснение:
Пусть х книг на второй полке, Тогда:
2х книг на третьей полке (в 2 раза больше, чем на второй) и
2х + 6 книг на первой полке (на 6 больше, чем на третьей)
Составим уравнение:
х + 2х + 2х + 6 = 216
5х = 216 - 6
5х = 210
х = 210/5
х = 42 книги на второй полке
42*2 = 84 книги на третьей полке
84 + 6 = 90 книг на первой полке
90+42+84 = 216 книг на трех полках
84/42 = 2 - на третьей полке книг в 2 раза больше, чем на второй
90 - 84 = 6 - на третьей полке на 6 книг меньше, чем на первой
Пошаговое объяснение:
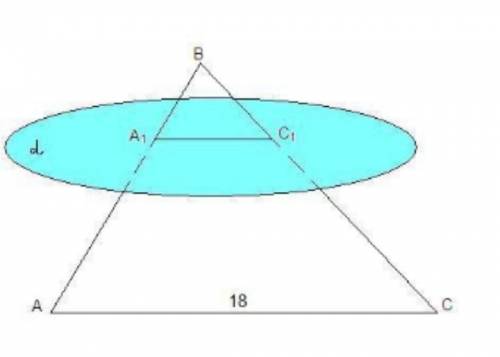
Плоскость α, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках А₁ и С₁ соответственно. Найдите отрезок А₁С₁, если АС = 18 см и АА₁:А₁В = 7:5.
7,5 см
Объяснение:
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Плоскость (АВС) проходит через прямую АС║α, значит плоскость (АВС) пересекает плоскость α по прямой, параллельной АС.
А₁С₁║АС.
Прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному, значит
ΔА₁ВС₁ ~ ΔАВС
По условию \dfrac{AA_{1}}{A_{1}B}=\dfrac{7}{5}
A
1
B
AA
1
=
5
7
то есть АА₁ составляет 7 частей, а А₁В - 5 частей, тогда АВ составляет 12 частей.
\dfrac{AC}{A_{1}C_{1}}=\dfrac{AB}{A_{1}B}=\dfrac{12}{5}
A
1
C
1
AC
=
A
1
B
AB
=
5
12
A_{1}C_{1}=\dfrac{5\cdot AC}{12}=\dfrac{5\cdot 18}{12}=\dfrac{15}{2}=7,5A
1
C
1
=
12
5⋅AC
=
12
5⋅18
=
2
15
=7,5 см
(x+6y)-(8x-7y) =x+6y-8x+7y=13y-6x
(m+n)-(m-n)=m+n-m+n=2n
(m+3)-(6m+5)-(m-1)=m+3-6m-5-m+1=-6m-1
(x-y)+(x-y)-(2x+y)= x-y+x-y-2x-y=-3y
(0,2x-3)-(x-2)-(0,4x-1)=0,2x-3-x-2-0,4x+1=-1,2x-4