Так, оскільки кути трикутників рівні.
Пошаговое объяснение:
Дано: a = 60, b = 40. a i b - відомі кути першого трикутника.
c = 80, d/e = 2/3. c,d,e - кути другого трикутника.
Розв'язок:
Нехай f - третій кут першого трикутника.
Тоді f = 180 - a - b = 80;
d + e + c = 180 => d + e = 180 - c = 100 => d = 100 - e =>
=> (100 - e) / e = 2 / 3 => (100 - e) * 3 = e * 2 =>
300 - 3e = 2e => 300 = 5e => e = 300 / 5 = 60;
d = 100 - e = 40;
a = e, b = d, c = e => кути трикутників рівні => трикутники подібні за
першою ознакою подібності трикутників.
Пусть окружность с центром O, вписанная в треугольник ABC, точками касания разбивает его стороны AB, AC и BC на отрезки AM+MB, AN+NC и BL+LC соответственно.
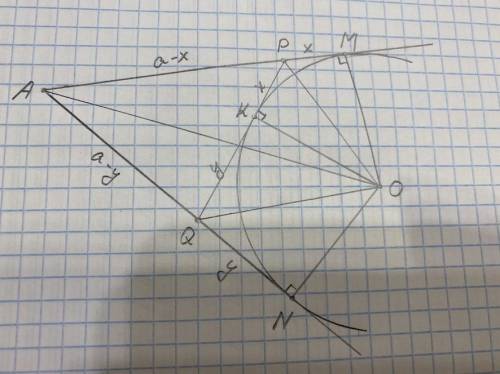
Рассмотрим часть треугольника при вершине A, которую отсекает вписанная в него окружность (см. рисунок).
Проведем произвольную касательную к окружности. Через K обозначим точку касания окружности, а через P и Q -- точки пересечения с отрезками AM и AN соответственно.
1. Докажем равенство отрезков AM = AN.
Рассмотрим треугольники OMA и ONA. Поскольку радиус, опущенный из центра окружности в точку касания, всегда перпендикулярен касательной, эти треугольники являются прямоугольными с прямым углом при вершинах M и N соответственно. Гипотенуза OA у треугольников OMA и ONA общая, а катеты OM и ON являются радиусами окружности и потому равны между собой. Таким образом, треугольники OMA и ONA равны, а следовательно AM = AN.
2. Докажем равенство отрезков PM = PK.
Рассмотрим треугольники OPM и OPK. По тем же соображениям они являются прямоугольными, имеют общую гипотенузу OP и равные катеты OM = OK. Таким образом, треугольники равны между собой, а следовательно PM = PK.
3. Докажем равенство отрезков QN = QK.
Рассмотрим треугольники OQN и OQK. По тем же соображениям они являются прямоугольными, имеют общую гипотенузу OQ и равные катеты ON = OK. Таким образом, треугольники равны между собой, а следовательно QN = QK.
4. Докажем, что сумма AM + AN длин отрезков , которые отсекает окружность от сторон треугольника ABC, равна периметру треугольника, который отсекает касательная PQ.
AM + AN = (AP + PM) + (AQ + QN) = (AP + PK) + (AQ + QK) = AP + PQ + AQ.
Рассуждения для двух оставшихся вершин B и C треугольника ABC полностью аналогичны.
Периметр треугольника ABC равен P = AB + AC + BC = (AM + MB) + (AN + NC) + (BL + LC) = (AM + AN) + (BM + BL) + (CN + CL), то есть сумме периметров треугольников, которые отсекают касательные к окружности.
Подставляя данные из условия задачи, находим, что P = 11 + 20 + 20 = 51.