(15 5/6 - 9 25/27)- (2/3 - 5/18) + 7/27 + 13/18=15 5/6 - 9 25/27- 2/3 + 5/18 + 7/27 + 13/18
1) 1) 5/18+13/18=1
2)7/27-9 25/27=-8 18/27
3) 15 5/6+5/18=15 15/18+5/18=16 1/9
4) 16 1/9-8 18/27=16 3/27-8 18/27=7 12/27=7 4/9
5) 7 4/9+1=8 4/9
(20 8/15 * 7 1/2-54 3/5 * 2/5):(3 13/21 * 8 2/5-29 2/5) - 5/6*1 1/5+21/25
1) 20 8/15 * 7 ½=308/15*15/2=154
2) 54 3/5 * 2/5=273/5*2/5=546/25=21.84
3) 154-21.84=132.16
4) 3 13/21 * 8 2/5=76/21*42/5=30.4
5) 30.4-29 2/5=30.4-29.4=1
6) 132.16:1=132.16
7) 5/6*1 1/5=5/6*6/5=1
8) 132.16-1=131.16
9) 131.16+21/25=131.16-0.84=130.32
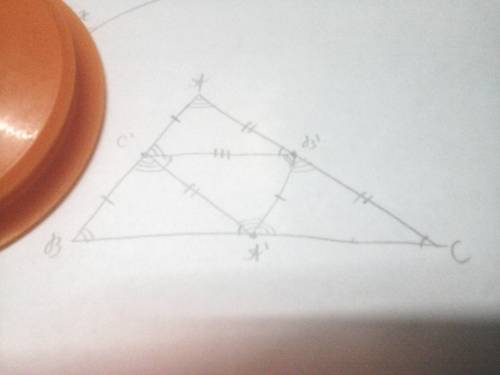
Есть треугольник ΔABC.
1) Найдём середину стороны AB, поставим там точку C'.
2) Проведём через C' прямую, параллельную стороне BC, в точке пересечения прямой и стороны AC поставим точку B'.
3) ∠C'BC = ∠AC'B', ∠BCB' = ∠C'B'A (соответственные углы), значит, ΔABC подобен ΔAC'B' (по трём углам), причём стороны ΔAC'B' в два раза меньше сторон ΔABC.
4) Проведём прямые, параллельные AB и AC через точки B' и C' соответственно. В точке пересечения этих прямых поставим точку A'.
5) ∠A'C'B' = ∠AB'C', ∠A'B'C' = ∠AC'B' (накрест лежащие углы), значит, ΔAC'B' = ΔA'B'C'.
6) Так как ∠AC'B' + ∠AB'C' + ∠C'AB' = 180° и ∠AC'B' + ∠A'C'B' + ∠A'C'B = 180°, то ∠C'A'B' = ∠C'AB' = ∠A'C'B. ∠B'C'A' = ∠C'A'B (накрест лежащие углы). По этим двум равенствам ΔB'C'A' = ΔBA'C'.
7) Для ΔCA'B' аналогично.
Мы разбили треугольник на 4 равных треугольника.